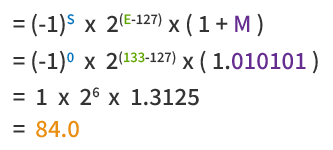一、浮點數是什麼？
浮點數（Floating-point number）是一種用有限的記憶體空間來近似表示小數或非常大的數的方法。「整數運算雖然速度更快且不會有四捨五入誤差，但整數型別無法方便地表示分數或極端範圍的數值」（Mitra, 2017，para. 2）。因此，我們需要浮點數來處理連續數值運算，例如科學計算中的物理常數或距離測量（如原子尺度、星系尺度）等，這些都難以用整數表示，因此基本上所有電腦系統的主流程式語言都支援浮點數型態。
[1]
二、浮點數的表示
浮點數的概念類似於科學記號
例如, 12345 如果用科學記號來計數，會寫成:
1.2345 × 10⁴
1.2345 叫做 尾數（fraction或mantissa），而 4 是 指數 (Exponent).
1.2345 x 10⁴以10為基數（Radix）是十進位制；而浮點數則是以2做為基數，為二進位制
以15為例：
| 整數(10進位) |
科學記號(10進位) |
浮點數(二進位) |
| 15 |
(1.5)10 × 101 |
(1.111)2 × 23 |
示範以浮點數表示15 這個數
步驟一：將 15 轉換為二進位
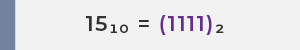
步驟二：把尾數的有效數字全部移到小數點後,換為形 (1.XXXX)₂ × 2ⁿ 的形式。
小數點向左移3位，為保持數值不變，基數2 要乘上3次方
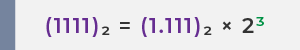
✅ 15 的浮點數表示為 :
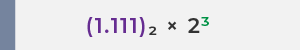
1. IEEE754 浮點數格式
為了避免換算浮點數時，平台之間產生不同的計算結果，根據維基百科（2024），自 1990 年代以來，大家普遍遵循IEEE（國際電機電子工程學會）在1985年制定的 IEEE 754標準（二進位浮點數算術標準）定義浮點數的表示和運算 ：
IEEE754 定義了：
- 浮點數的存儲格式（如 32 位元（Float32） 和 64 位元（Float64））。
- 浮點數的運算行為（如捨入模式、特殊值 NaN、無窮大等）。
- 浮點數的特殊狀況（如 溢出（Overflow）、下溢（Underflow）、除零錯誤）。
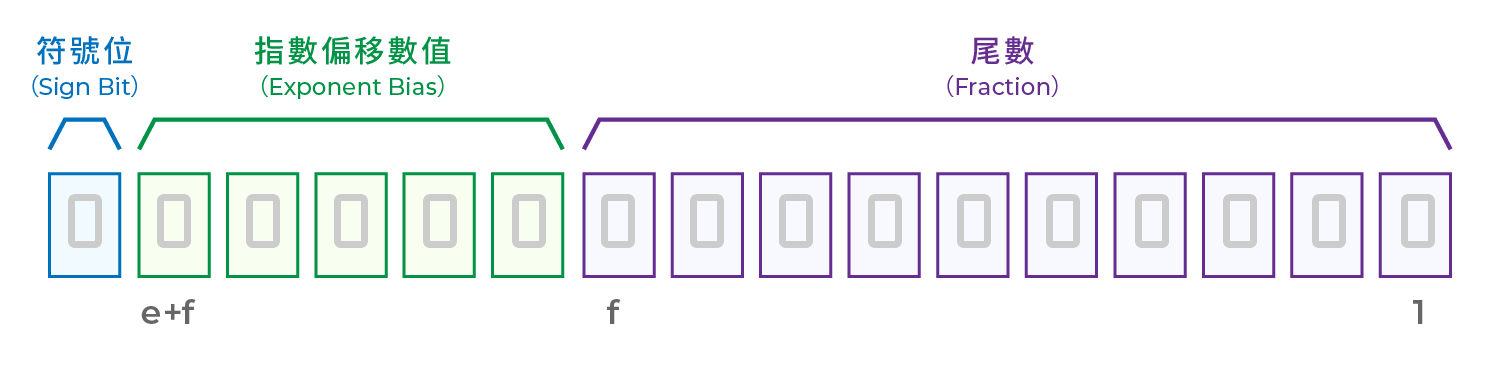
IEEE754 將浮點數計數格式定義為：
值 = (−1)符號位 × 2指数 × (1 + 分数值)
符號位（Sign Bit）: 1 位，決定數字的正負：0 = 正數／1 = 負數
指數偏移數值（Exponent bias）: 用來控制數值的範圍（以 2 為底的次方），為指數偏移值减去偏移量（bias）。
尾數（fraction）: 尾數為「1+分數值」，存儲有效數字（類似科學記數法中的「1.XX」）。
2. 浮點數精度：單精度 Float32 ＆ 雙精度 Float64
15 的浮點數表示為
(1.111)₂× 2³，寫作
(−1)⁰ × 2³ × (1.111)₂
符合 IEEE 754 的標準化表示方式，而電腦在存儲浮點數時，是根據 IEEE 754 單精度（Float32） 或 雙精度（Float64） 存儲格式進行編碼。
1) 單精度（Single Precision）
每當存儲浮點數時，首位的 1 被默認存在，因此不需存儲整個有效數字（significand），而僅存儲小數部分（fractional part）。
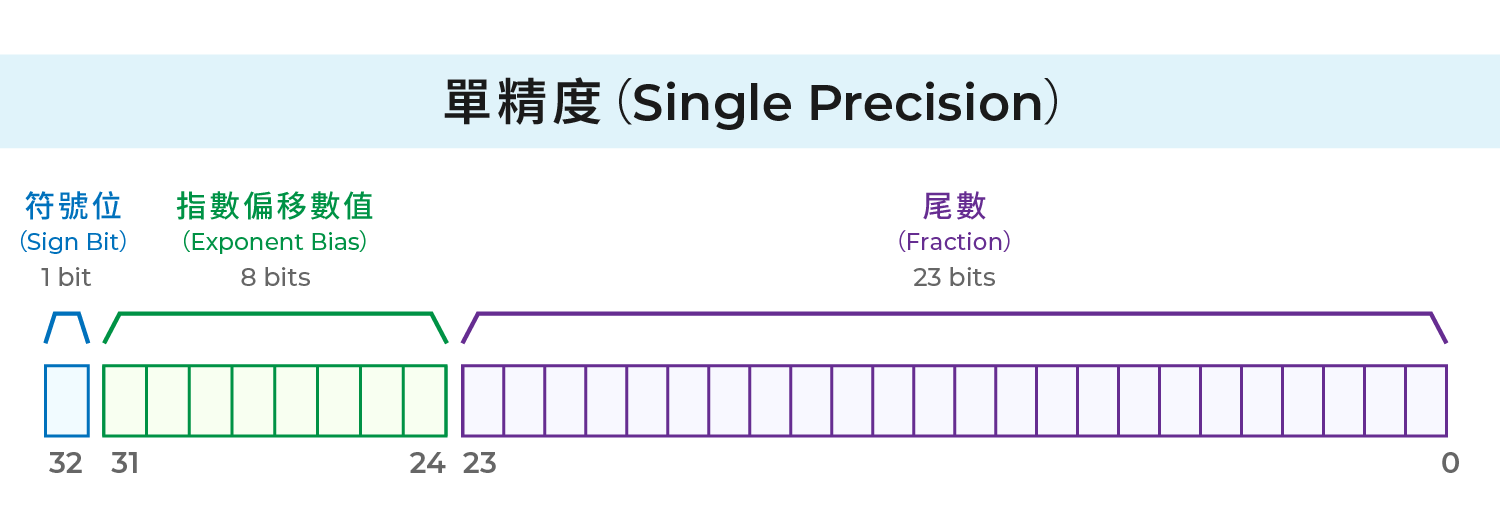
IEEE754 單精度共 32bit:
1 bit: 符號位（sign bit）
8 bits: 指數位（exponent, m）
23 bits: 尾數（fraction, f）
單精度指數被偏移 127，以避免存儲負號。電腦存儲的不是
m，而是
m + 127。因此，指數的最大可能值為 127，最小可能值為 -126。
(Grainger College of Engineering, 2019)
* 運算範例請參考下一章節
2) 雙精度（Double Precision）
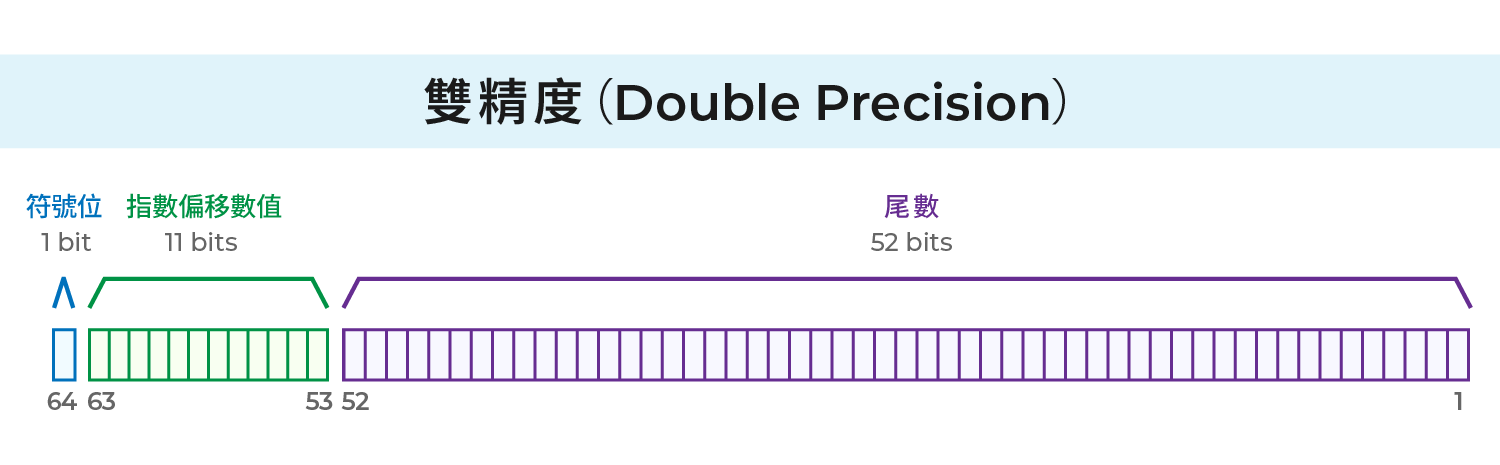
IEEE754 雙精度共 64bit:
1 bit: 符號位（sign bit）
11 bits: 指數位（exponent, m）
52 bits: 尾數（fraction, f）
雙精度指數被偏移 1023 以避免存儲負號。電腦存儲的不是 m，而是 m + 1023。因此，指數的最大可能值為 1023，最小可能值為 -1022。
(Grainger College of Engineering, 2019)
3) Float32 vs Float64 特性比較
| 特性 |
Float32（單精度） |
Float64（雙精度） |
| 位元數 |
32 bits |
64 bits |
| 尾數長度 |
23 bits（約 7–8 位十進位數字） |
52 bits（約 15–16 位十進位數字） |
| 指數長度 |
8 bits（偏移量 127） |
11 bits（偏移量 1023） |
| 可表示範圍 |
約 10⁻³⁸ ~ 10³⁸ |
約 10⁻³⁰⁸ ~ 10³⁰⁸ |
| 記憶體占用 |
4 bytes（32-bit） |
8 bytes（64-bit） |
| 運算速度 |
較快（適用於圖形處理、AI 訓練等） |
較慢（但更精確，適用於科學計算） |
| 常見應用 |
● 遊戲開發、圖形處理（GPU 計算）
● 機器學習（如 TensorFlow 使用混合精度計算）
● 數據量大但精度要求不高的應用
|
● 科學計算、模擬（如天氣預報、物理模擬）
● 金融運算（避免捨入誤差）
● 高精度數值計算（如工程應用）
|
三、32bit浮點數運算範例
| 單精度（Float32, 32-bit）格式 |
| 部分 |
位數 |
說明 |
| 符號位（S） |
1 bit |
0（正數） |
| 指數位（E） |
8 bits |
3 + 127 = 130 = 10000010₂ |
| 尾數位（M） |
23 bits |
11100000000000000000000（去掉 1.，只存 111） |
| 儲存 |
32 bits |
0 10000010 11100000000000000000000 |
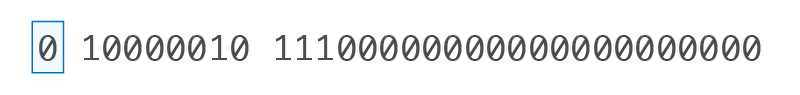• 符號位（Sign Bit, S）：0
(−1)⁰=1（表示是正數）
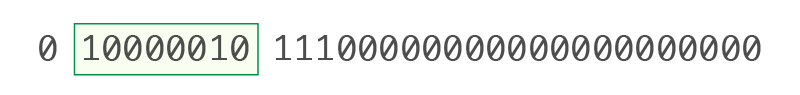• 指數位（Exponent, E）（第2到第9位）：10000010
轉換成十進位：10000010₂ =130₁₀
*IEEE 754 使用偏移量Bias = 127
130 - 127 = 3
所以 指數值 = 3，即 2³
(*IEEE 754 使用偏移量Bias ，以單精度浮點數（32 位元）為例，指數部分佔用 8 位元。根據 IEEE 754 的定義，偏移量計算公式為：Bias= 2ᵉ⁻¹-1，因此單精度浮點數的 Bias= 2⁸⁻¹-1=127)
• 尾數位（fraction, M）：11100000000000000000000
IEEE 754 規定尾數是 「1+分數值」(隱含 1 的標準化形式)，所以實際的尾數是：1.11100000000000000000000₂
轉換為十進位:
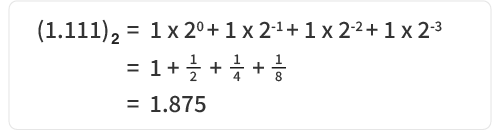
IEEE754 將浮點數計數格式定義為::
四、Ｍodbus 浮點數存取與轉換
在 Modbus 通信中，數據以暫存器（Register）的形式存儲，每個暫存器為 16 位元。然而，以浮點數單精度為例，需要 32 位來表示，面對這樣的情況，在不改變 Modbus 基本架構的前提下，當需要傳輸超過16位元的數據時，就需要佔用多個連續的寄存器地址。單精度浮點數(32bit）需使用兩個相鄰的寄存器來存放。
Modbus 協議在傳輸多位元數值時規定使用大端序 (Big-Endian) 表示法。所謂大端序是指當傳送一個超過1 byte的數值時，先傳送高序位元組。例如，16位元值 0x1234（十六進制）在總線上的傳輸順序將先後送出 0x12 和 0x34 （Modbus Organization, 2006）。
[4]
1.Ｍodbus 如何存放一個32位浮點數
浮點數 84.0，如何在 Modbus中儲存?
• 轉換為 IEEE 754 單精度浮點數：
84.0 的 IEEE 754 單精度（32-bit）二進位表示為：
01000010101010000000000000000000₂
• 轉換為十六進位： 0x42A80000
• 在 Modbus 中的存放方式（大端序）：
Modbus 每個寄存器為 16bit，因此單精度浮點數(32bit)會拆成兩個寄存器存放：
高位寄存器（前 16-bit）: 0x42A8
低位寄存器（後 16-bit）: 0x0000
2.Modbus 數值如何解碼回浮點數值
假設：
設備地址（Slave ID）: 0x01
功能碼（Function Code）: 0x03（讀取保持暫存器 Holding Registers）
寄存器起始地址: 0x1000
讀取寄存器數量: 0x0002（因為單精度浮點數佔 2 個 16-bit 暫存器）
➤ Modbus 傳輸請求（TX - Master 發送數據）：
01 03 10 00 00 02 C5 CD
| 位元組 |
說明 |
值 |
| 01 |
設備地址(Slave ID) |
0x01 |
| 03 |
讀取保持暫存器 |
0x03 |
| 10 00 |
起始地址(0x1000) |
0x1000 |
| 00 02 |
讀取2個暫存器 |
0x0002 |
| C5 CD |
CRC-16 校驗碼 |
0xC5CD |
➤ Modbus 設備回應（RX - Slave 回應數據）:
01 03 04 42 A8 00 00 79 32
| 位元組 |
說明 |
值 |
| 01 |
設備地址(Slave ID) |
0x01 |
| 03 |
功能碼(讀取 Holding Registers) |
0x03 |
| 04 |
資料位元組數
|
0x04 (4 bytes = 32-bit) |
| 42 A8 |
高位寄存器值 |
0x42A8 |
| 00 00 |
低位寄存器值 |
0x0000 |
| 79 32 |
CRC-16 校驗碼 |
0x7932 |
可以看到合併寄存器數據:
高位為16-bit = 0x42A8，低位為 16-bit = 0x0000
組合為 32-bit 整數（默認為大端序模式）：0x42A80000
二進位表示：0100 0010 1010 1000 0000 0000 0000 0000
拆解 IEEE 754 組成部分
• 符號位（S） = 0 (正數)
• 指數位（E） = 10000101₂ = 133
• 尾數位（M）= 01010000000000000000000₂
帶入 IEEE 754 計算公式，得出十進位數值
84.0：
