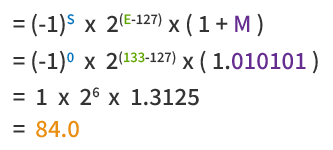1. 浮動小数点数とは？
浮動小数点数とは、限られたメモリ空間で小数や非常に大きな数値を表現するための方法です。Mitra（2017年、段落2）によると、「整数演算は高速で丸め誤差が発生しないが、分数や極端な範囲の値を表現するには適していない」とされています。
そのため、浮動小数点数が必要になります。連続的な数値データをより効果的に扱えるようになり、物理定数の表現や、原子スケールや銀河スケールの距離を測るといった科学的計算に特に役立ちます。このような値は整数では表現が難しい、あるいは不可能です。そのため、ほぼすべての現代的なプログラミング言語は浮動小数点データ型を標準でサポートしています。
[1]
2. 浮動小数点数の表現方法
浮動小数点数は、科学的記数法とよく似た形式で表現されます。
たとえば、数値 12345 は科学的記数法で次のように表されます：
1.2345 × 10⁴
ここで、1.2345 は 仮数部（mantissa）、4 は 指数部（exponent）と呼ばれます。
科学的記数法は 10 進数（基数10）を使いますが、浮動小数点数は 2 進数（基数2）を使用します。
例として、数値 15 を見てみましょう：
| 整数（10進数） |
科学的記数法（10進数） |
浮動小数点（2進数） |
| 15 |
(1.5)10 × 101 |
(1.111)2 × 23 |
例：15 を浮動小数点数として表す場合
ステップ1：15 を2進数に変換
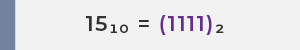
ステップ2：仮数のすべての有効数字を小数点の右側にシフトして、(1.XXXX)₂ × 2ⁿ の形にする
小数点を左に3桁移動させると、値を維持するために基数2を3乗する必要があります
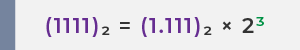
✅ 最終的な浮動小数点表現：
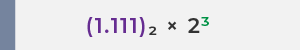
1 ) IEEE 754 浮動小数点形式
異なるプラットフォーム間で浮動小数点の結果が不一致にならないようにするため、IEEE（米国電気電子学会）は1985年に IEEE 754 標準を策定しました。1990年代以降、この標準は広く採用され、浮動小数点数の表現と計算方法を定義するために使われています(Wikipedia, 2024):
IEEE 754 は以下を定義しています：
- 浮動小数点数の記憶形式（例：32ビットの Float32、64ビットの Float64）
- 浮動小数点演算のルール（例：丸めモード、NaNや無限大などの特殊値）
- 例外的なケース（例：オーバーフロー、アンダーフロー、0除算など）
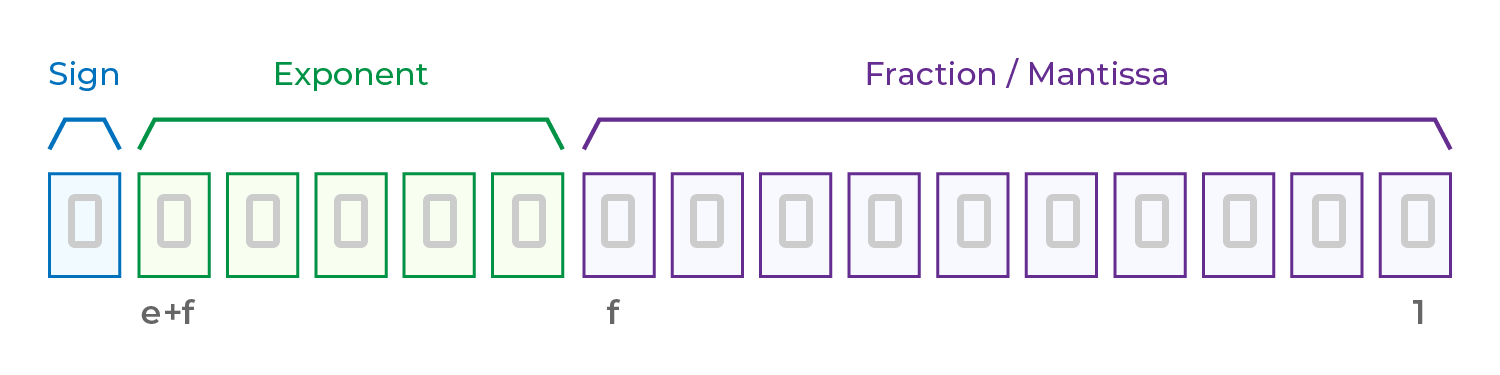
IEEE 754 によって浮動小数点数の構造は次のように定義されます：
値 = (−1)符号 × 2指数 × (1 + 仮数)
符号ビット( Sign ): 1ビットで、数値が正か負かを示します：0 = 正 / 1 = 負
指数バイアス ( Exponent Bias ): 値の範囲（2の累乗）を制御するために使用され、実際の指数からバイアス値を引いて計算されます。
仮数 / マンティッサ (Mantissa): "1 + 小数部分" を表し、科学的記数法の "1.XX" のように有効桁を保存します。
2 ) 浮動小数点の精度：Float32 と Float64
15 の浮動小数点表現は
(1.111)₂ × 2³ であり、次のように表されます：
(−1)⁰ × 2³ × (1.111)₂
これは IEEE 754 の正規化形式に従っています。コンピュータが浮動小数点数を保存する際は、IEEE 754 規格に従って、単精度（Float32）または倍精度（Float64）としてエンコードされます。
単精度
浮動小数点数を保存する際、先頭の 1 は省略されるのが前提です。そのため、仮数全体ではなく、小数点以下の部分だけが保存されます。
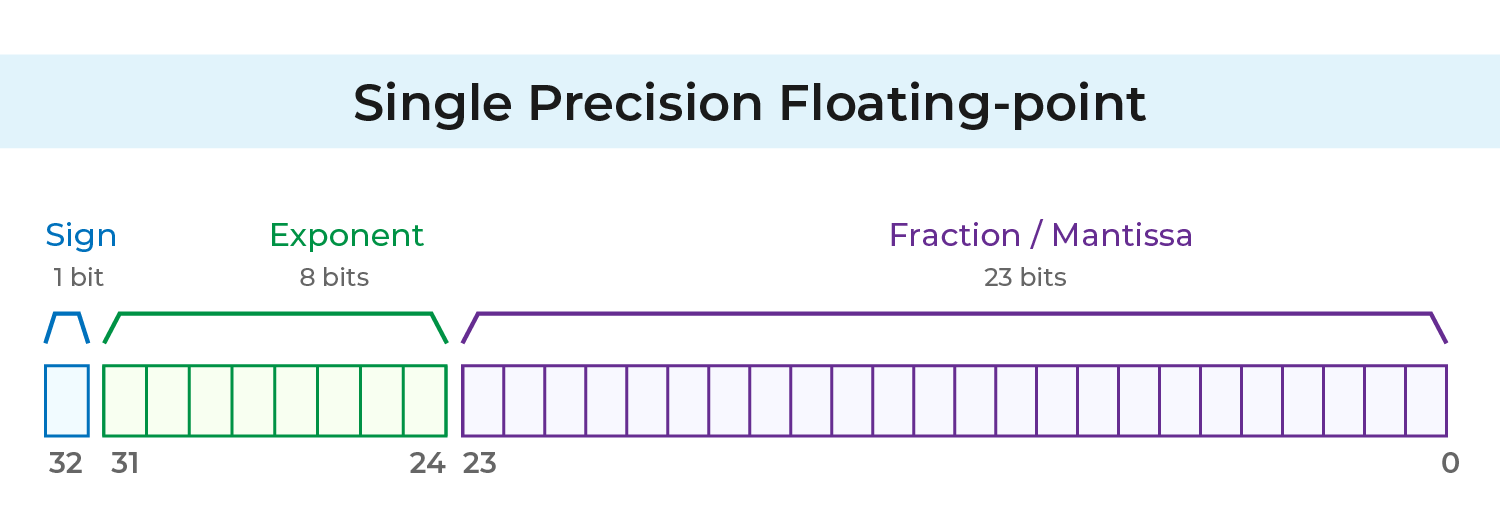
IEEE 754 の単精度形式では、合計で32ビットを使用します：
1ビット: 符号ビット
8 ビット: 指数（m）
23 ビット: 仮数（f）
単精度の場合、指数には − を含む負の値を避けるため、127 のバイアスが加えられます。つまり、コンピュータは実際の
m ではなく
m + 127 を保存します。
したがって、指数の最大値は127、最小値は −126 です。
(Grainger College of Engineering, 2019)
※ 計算例については次のセクションをご参照ください。
倍精度
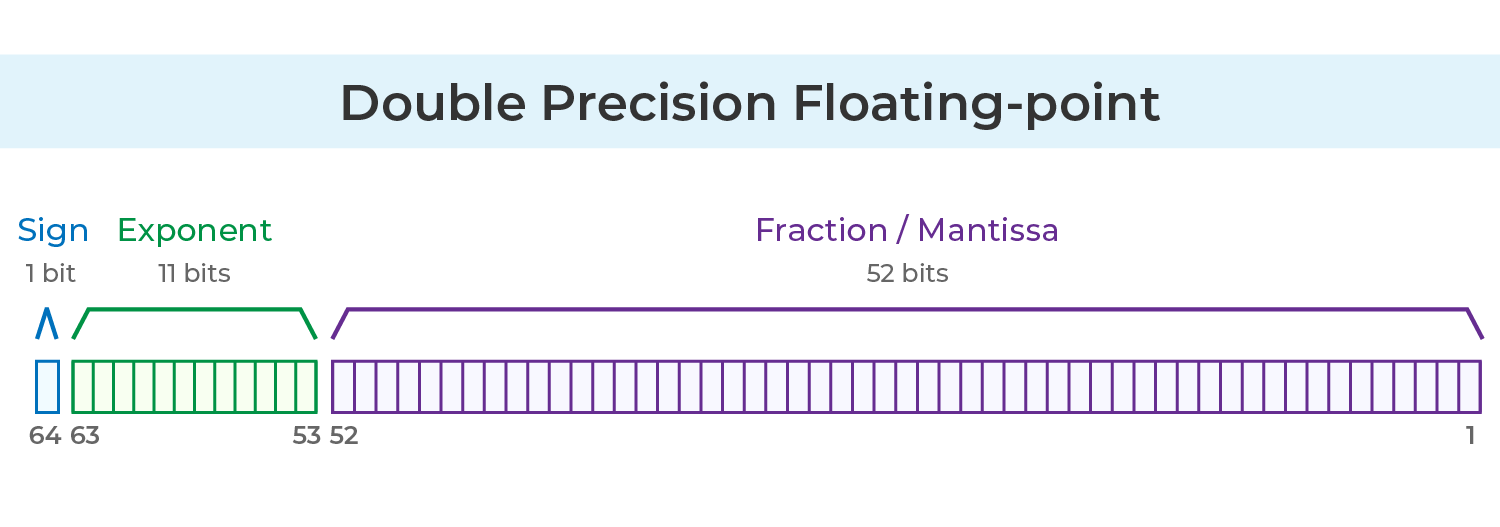
IEEE 754 の倍精度形式では、合計で64ビットを使用します：
1 ビット: 符号ビット
11 ビット: 指数（m）
52 ビット: 仮数（f）
倍精度の場合、指数には 1023 のバイアスが加えられます。つまり、コンピュータは実際の m ではなく m + 1023 を保存します。そのため、指数の最大値は1023、最小値は −1022 です。
(Grainger College of Engineering, 2019)
Float32 と Float64 の機能比較
| 項目 |
Float32（単精度） |
Float64（倍精度） |
| ビット長 |
32ビット |
64ビット |
| 仮数部の長さ |
23ビット（約7〜8桁の10進精度） |
52ビット（約15〜16桁の10進精度） |
| 指数部の長さ |
8ビット（バイアス：127） |
11ビット（バイアス：1023） |
| 表現可能な値の範囲 |
約 10⁻³⁸ ～ 10³⁸ |
約 10⁻³⁰⁸ ～ 10³⁰⁸ |
| メモリ使用量 |
4バイト（32ビット） |
8バイト（64ビット） |
処理性能
|
高速（グラフィック処理、AI学習に最適） |
低速だが高精度（科学技術計算に最適） |
| 主な用途 |
• ゲーム開発、グラフィック処理（GPUコンピューティング）
• 機械学習（例：TensorFlow における混合精度）
• 精度をあまり必要としない大規模データセット |
• 科学技術計算およびシミュレーション（例：天気予測、物理モデリング）
• 金融計算（丸め誤差の回避）
• 高精度な数値計算（例：工学分野の応用） |
3. 32ビット浮動小数点の計算例
| 単精度（Float32、32ビット）フォーマット |
構成要素
|
ビット数 |
説明 |
| 符号ビット（S） |
1 ビット |
0（正） |
| 指数（E） |
8 ビット |
3 + 127 = 130 = 10000010₂ |
| 仮数（M） |
23 ビット |
11100000000000000000000（先頭の 1. を省略して保存） |
| 格納形式 |
32 ビット |
0 10000010 11100000000000000000000 |
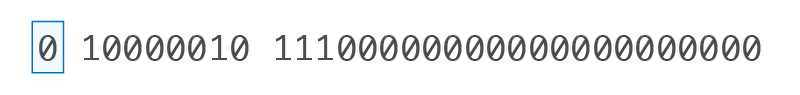• 符号ビット（S）：0
(−1)⁰ = 1（正の数を示す）
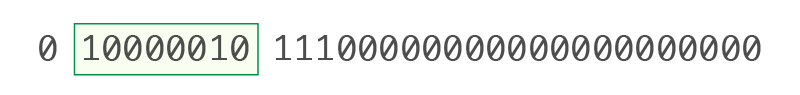• 指数（E）（ビット2〜9）：10000010
10進数に変換すると：10000010₂ = 130₁₀
*IEEE 754ではバイアス値127を使用
130 - 127 = 3
つまり、指数 = 3 → 23
（※IEEE 754では指数をバイアス形式で表します。単精度では指数部に8ビットが割り当てられ、バイアス = 2⁸⁻¹ − 1 = 127）
• 仮数（M）：11100000000000000000000
IEEE 754 によると、仮数は「1 + 小数部」の正規化形式を使用するため、実際の値は：1.11100000000000000000000₂ になります。
10進数に変換 :
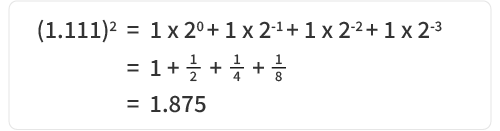
IEEE754 浮動小数点形式は次のように定義されます：
値 = (−1)符号 × 2指数 × (1 + 仮数)
= (−1)0 × 23 × (1 + 0.875)
= 15
4. Modbusにおける浮動小数点のアクセスと変換
Modbus通信では、データは16ビット幅のレジスタに格納されます。しかし、単精度の浮動小数点数を表現するには32ビットが必要です。Modbusの構造内でこれを扱うためには、16ビットを超えるデータを複数の連続したレジスタにまたがって格納する必要があります。つまり、32ビットの浮動小数点は2つの隣接レジスタを使用します。
Modbusプロトコルでは、マルチバイト値の送信にはBig-Endian形式が指定されています。Big-Endianでは、最上位バイトが先に送信されます。たとえば、16ビットの16進数 0x1234 は、バス上では 0x12、続いて 0x34 の順に送信されます。(Modbus Organization, 2006)
[4]
1 ) Modbusで32ビット浮動小数点を格納する方法
Modbusで浮動小数点値 84.0 をどのように格納するか？
• IEEE 754 単精度フォーマットに変換：
85.625 の IEEE 754 単精度（32ビット）バイナリ表現は：
01000010101010000000000000000000₂
• 16進数に変換：0x42A80000
• Modbusでの格納（Big-Endian形式）：
Modbusの各レジスタは16ビットのため、32ビットのfloatは2つのレジスタに分割されます：
上位レジスタ（最初の16ビット）：0x42A8
下位レジスタ（最後の16ビット）：0x0000
2 ) Modbusの値を浮動小数点に復元する方法
例：
デバイスアドレス（スレーブID）：0x01
ファンクションコード：0x03（ホールディングレジスタの読み取り）
開始レジスタアドレス：0x1000
読み取るレジスタ数：0x0002（32ビットのfloatは16ビット×2のため）
➤ Modbus送信要求（TX - マスタが送信）：
01 03 10 00 00 02 C5 CD
| バイト |
説明 |
値 |
| 01 |
デバイスアドレス（スレーブID） |
0x01 |
| 03 |
ファンクションコード（ホールディングレジスタ読み取り） |
0x03 |
| 10 00 |
開始アドレス（0x1000） |
0x1000 |
| 00 02 |
読み取るレジスタ数（2つ） |
0x0002 |
| C5 CD |
CRC-16チェックサム |
0xC5CD |
➤ Modbus応答（RX - スレーブが応答）：
01 03 04 42 A8 00 00 79 32
| バイト |
説明 |
値 |
| 01 |
デバイスアドレス（スレーブID） |
0x01 |
| 03 |
ファンクションコード（ホールディングレジスタ読み取り）
|
0x03 |
| 04 |
バイト数 |
0x04 （4バイト = 32ビット) |
| 42 A8 |
上位レジスタの値 |
0x42A8 |
| 00 00 |
下位レジスタの値
|
0x0000 |
| 79 32 |
CRC-16チェックサム
|
0x7932 |
上記の通り、結合されたレジスタデータは以下の通りです：
上位16ビット = 0x42A8、下位16ビット = 0x0000
これを32ビット値として結合（Big-Endian）すると：0x42A80000
2進数表現：0100 0010 1010 1000 0000 0000 0000 0000
IEEE 754 の分解：
• 符号ビット（S）= 0 （正）
• 指数（E）= 10000101₂ = 133
• 仮数（M）= 01010000000000000000000₂
IEEE 754 の数式に代入すると、10進数値は：
84.0
