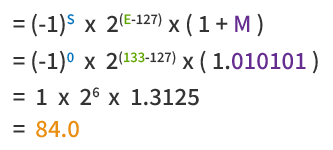1. เลขทศนิยมลอยคืออะไร?
เลขทศนิยมลอยคือวิธีหนึ่งในการแทนค่าตัวเลขทศนิยมหรือค่าที่มีขนาดใหญ่มาก โดยใช้หน่วยความจำที่จำกัด ตามที่ Mitra (2017, ย่อหน้า 2) ระบุไว้ว่า "แม้ว่าการดำเนินการกับจำนวนเต็มจะเร็วกว่าและไม่มีข้อผิดพลาดจากการปัดเศษ แต่จำนวนเต็มไม่เหมาะสำหรับการแทนค่าทศนิยมหรือค่าที่มีช่วงกว้างมาก"
ดังนั้นจึงต้องใช้เลขทศนิยมลอย ซึ่งช่วยให้เราสามารถจัดการข้อมูลเชิงตัวเลขแบบต่อเนื่องได้อย่างมีประสิทธิภาพ โดยเฉพาะในงานคำนวณทางวิทยาศาสตร์ เช่น การแทนค่าคงที่ทางฟิสิกส์ หรือการวัดระยะทางในระดับอะตอมหรือกาแล็กซี ซึ่งค่าประเภทนี้ไม่สามารถใช้จำนวนเต็มแทนได้อย่างเหมาะสม นั่นจึงเป็นเหตุผลที่ภาษาโปรแกรมสมัยใหม่เกือบทั้งหมดรองรับประเภทข้อมูลแบบเลขทศนิยมลอย
[1]
2. รูปแบบการแสดงเลขทศนิยมลอย
ตัวเลขแบบ Floating-point ทำงานคล้ายกับเลขแบบ Scientific notation (เลขยกกำลังฐานสิบ)
ตัวอย่างเช่น ตัวเลข 12345 ถ้าเขียนในรูปแบบ Scientific notation จะเป็น
1.2345 × 10⁴
ตรงนี้ 1.2345 คือ ส่วนเศษ (mantissa) และ 4 คือ เลขชี้กำลัง (exponent)
Scientific notation ใช้ ฐาน 10 (decimal)
แต่ Floating-point number ใช้ ฐาน 2 (binary)
ลองดูตัวอย่างของเลข 15:
| เลขจำนวนเต็ม (ฐาน 10) |
Scientific Notation (ฐาน 10) |
Floating-point (ฐาน 2) |
| 15 |
(1.5)10 × 101 |
(1.111)2 × 23 |
ตัวอย่าง: แสดงเลข 15 ในรูปแบบ Floating-point
ขั้นตอนที่ 1: แปลงเลข 15 เป็นเลขฐานสอง (Binary)
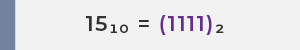
ขั้นตอนที่ 2: เลื่อนตำแหน่งทศนิยมไปทางซ้ายให้เฉพาะเลขสำคัญ (mantissa) อยู่ด้านขวาของจุดทศนิยม เพื่อให้อยู่ในรูป (1.XXXX)₂ × 2ⁿ
เลื่อนจุดทศนิยมไปทางซ้าย 3 ตำแหน่ง และเพิ่มเลขชี้กำลังของฐาน 2 เป็น 3 เพื่อให้ค่าคงเดิม
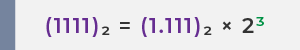
✅ ผลลัพธ์สุดท้ายในรูปแบบ Floating-point:
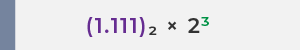
1 ) รูปแบบเลขทศนิยมลอย IEEE 754
เพื่อหลีกเลี่ยงผลลัพธ์ของเลขทศนิยมลอยที่ไม่สอดคล้องกันในแต่ละแพลตฟอร์ม IEEE (สถาบันวิศวกรไฟฟ้าและอิเล็กทรอนิกส์) ได้เสนอข้อกำหนด IEEE 754 ในปี 1985 และถูกนำไปใช้อย่างแพร่หลายตั้งแต่ปี 1990 เป็นต้นมา โดยข้อกำหนดนี้ใช้ในการกำหนดวิธีเก็บและคำนวณเลขทศนิยมลอย (Wikipedia, 2024):
IEEE 754 กำหนดว่า:
- รูปแบบการจัดเก็บเลขทศนิยมลอย (เช่น 32-bit Float32 และ 64-bit Float64)
- กฎการดำเนินการกับเลขทศนิยมลอย (เช่น โหมดการปัดเศษ, ค่าพิเศษอย่าง NaN และ Infinity)
- กรณีข้อยกเว้น (เช่น overflow, underflow และการหารด้วยศูนย์)
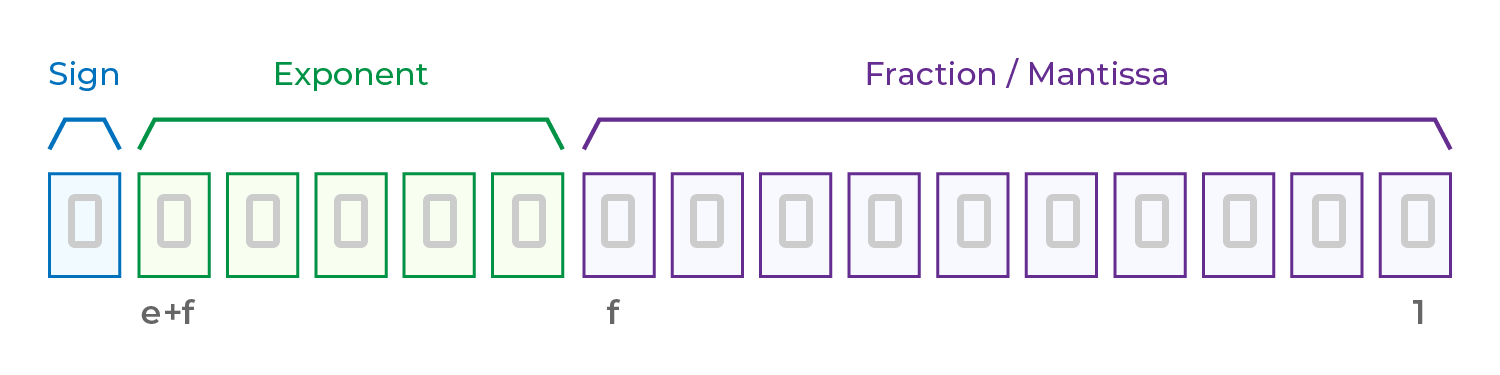
IEEE 754 กำหนดโครงสร้างของเลขทศนิยมลอยดังนี้:
ค่า = (−1)sign × 2exponent × (1 + fraction)
บิตสัญลักษณ์ (Sign Bit): 1 บิต ใช้กำหนดว่าเลขเป็นบวกหรือเป็นลบ: 0 = บวก / 1 = ลบ
ค่าชดเชยเลขชี้กำลัง (Exponent Bias): ใช้ควบคุมช่วงค่าของเลข (เป็นกำลังของ 2) โดยคำนวณจากเลขชี้กำลังลบด้วยค่า bias
เศษส่วน (Mantissa): แทนค่า "1 + ส่วนเศษ" และเก็บเลขสำคัญที่ใช้ในการคำนวณ (คล้ายรูปแบบ "1.XX" ในเลขยกกำลัง)
2 ) ความแม่นยำของเลขทศนิยมลอย: Float32 และ Float64
รูปแบบเลขทศนิยมลอยตัวของ
15 คือ
(1.111)₂ × 2³ ซึ่งเขียนได้เป็น
(−1)⁰ × 2³ × (1.111)₂
รูปแบบนี้เป็นไปตามมาตรฐาน IEEE 754 แบบ normalized ซึ่งคอมพิวเตอร์จะจัดเก็บค่าทศนิยมลอยตัวตามมาตรฐานนี้ โดยใช้ความละเอียดแบบ single precision (Float32) หรือ double precision (Float64)
ความแม่นยำระดับเดียว (Single Precision)
เมื่อจัดเก็บค่าทศนิยมลอย ตัวเลข 1 ที่นำหน้าจะถูกสมมุติไว้โดยอัตโนมัติ ดังนั้นจะจัดเก็บเฉพาะส่วนเศษหลังจุดทศนิยม ไม่ใช่ทั้งหมดของ mantissa
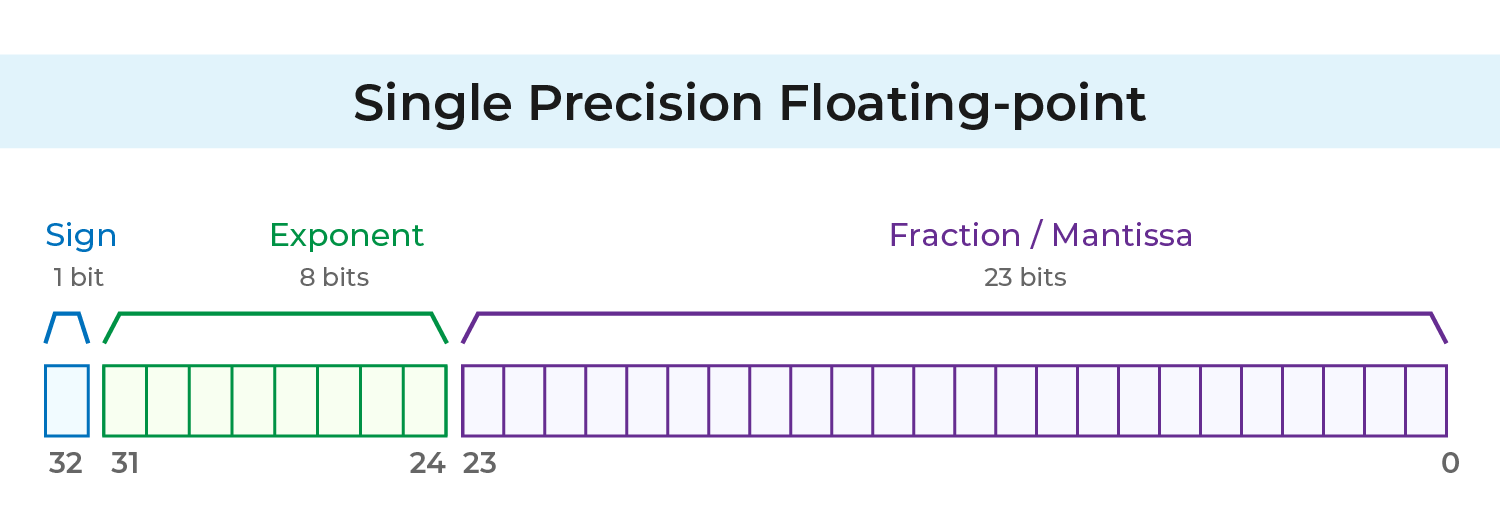
รูปแบบ single precision ตาม IEEE 754 ใช้ทั้งหมด 32 บิต:
1 บิต: บิตเครื่องหมาย
8 บิต: เลขชี้กำลัง (m)
23 บิต: ส่วนเศษ (f)
ในรูปแบบความแม่นยำระดับเดียว ค่า exponent จะมี bias เท่ากับ 127 เพื่อหลีกเลี่ยงการจัดเก็บเครื่องหมายลบโดยตรง ดังนั้นระบบจะจัดเก็บเป็น m + 127 แทน m
ค่าชี้กำลังสูงสุดคือ 127 และค่าต่ำสุดคือ −126
(Grainger College of Engineering, 2019)
* ตัวอย่างการคำนวณจะอยู่ในส่วนถัดไป
ความแม่นยำสองระดับ (Double Precision)
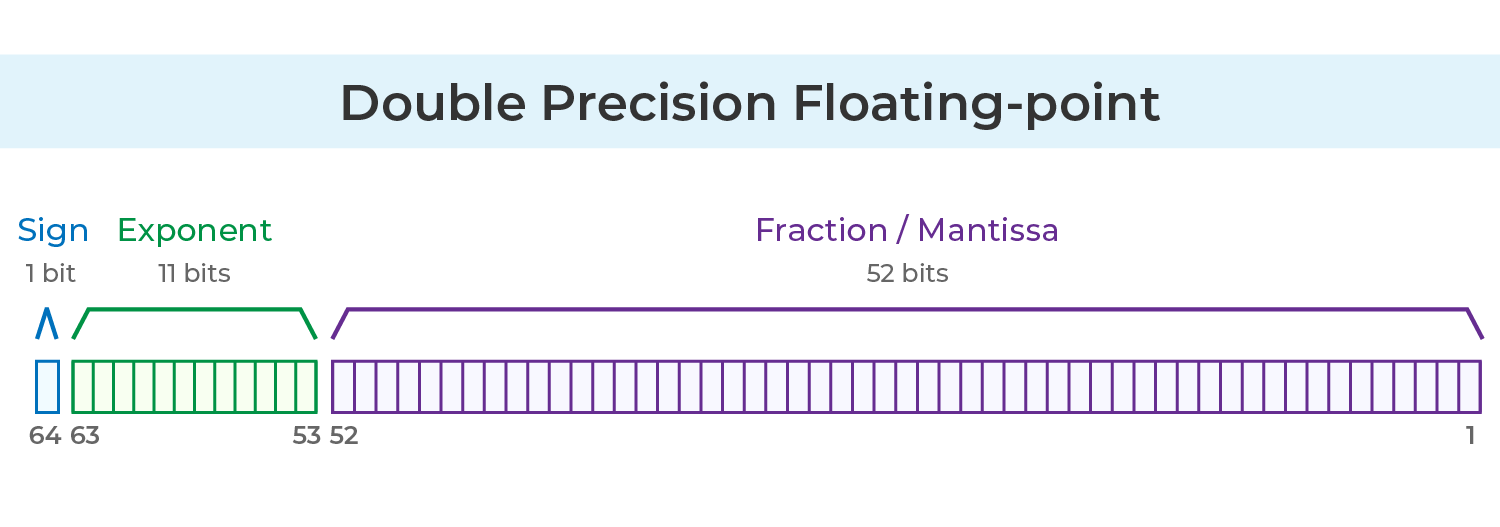
IEEE 754 ความแม่นยำสองระดับใช้ทั้งหมด 64 บิต:
1 บิต: บิตเครื่องหมาย
11 บิต: เลขชี้กำลัง (m)
52 บิต: ส่วนเศษ (f)
ในรูปแบบ double precision ค่า exponent มี bias เท่ากับ 1023 ดังนั้นระบบจะจัดเก็บเป็น m + 1023 แทน m
ค่าชี้กำลังสูงสุดคือ 1023 และต่ำสุดคือ −1022
(Grainger College of Engineering, 2019)
การเปรียบเทียบคุณสมบัติของ Float32 กับ Float64
| คุณสมบัติ |
Float32 (ความแม่นยำเดี่ยว) |
Float64 (ความแม่นยำสองเท่า) |
| ความยาวบิต |
32 บิต |
64 บิต |
| ความยาวส่วนเศษ |
23 บิต (ประมาณ 7–8 หลักทศนิยม) |
52 บิต (ประมาณ 15–16 หลักทศนิยม) |
| ความยาวเลขชี้กำลัง |
8 บิต (bias: 127) |
11 บิต (bias: 1023) |
| ช่วงของค่า |
ประมาณ 10⁻³⁸ ~ 10³⁸ |
ประมาณ 10⁻³⁰⁸ ~ 10³⁰⁸ |
| การใช้หน่วยความจำ |
4 ไบต์ (32 บิต) |
8 ไบต์ (64-บิต) |
| ประสิทธิภาพ |
เร็วกว่า (เหมาะกับการประมวลผลกราฟิก, การฝึก AI) |
ช้ากว่าแต่แม่นยำกว่า (เหมาะกับการคำนวณทางวิทยาศาสตร์) |
| การใช้งานทั่วไป |
• การพัฒนาเกม, การประมวลผลกราฟิก (GPU computing)
• การเรียนรู้ของเครื่อง (เช่น mixed precision ใน TensorFlow)
• ชุดข้อมูลขนาดใหญ่ที่ไม่ต้องการความแม่นยำสูง |
• การคำนวณทางวิทยาศาสตร์และการจำลอง (เช่น พยากรณ์อากาศ, การจำลองทางฟิสิกส์)
• การคำนวณทางการเงิน (เพื่อหลีกเลี่ยงข้อผิดพลาดจากการปัดเศษ)
• การคำนวณตัวเลขที่ต้องการความแม่นยำสูง (เช่น วิศวกรรม) |
3. ตัวอย่างการคำนวณแบบ Floating-Point 32 บิต
| รูปแบบความแม่นยำเดี่ยว (Float32, 32 บิต) |
| องค์ประกอบ |
จำนวนบิต |
คำอธิบาย |
| บิตเครื่องหมาย (S) |
1 บิต |
0 (บวก) |
| เลขชี้กำลัง (E) |
8 บิต |
3 + 127 = 130 = 10000010₂ |
| เศษส่วน (M) |
23 บิต |
11100000000000000000000 (ละเว้น 1. ด้านหน้า เก็บเฉพาะ 111) |
| ข้อมูลที่จัดเก็บ |
32 บิต |
0 10000010 11100000000000000000000 |
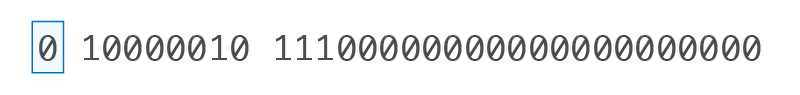• บิตเครื่องหมาย (S): 0
(−1)⁰ = 1 (แสดงว่าเป็นจำนวนบวก)
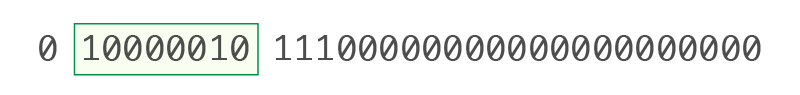• เลขชี้กำลัง (E) (บิตที่ 2–9): 10000010
แปลงเป็นเลขฐานสิบ: 10000010₂ = 130₁₀
*มาตรฐาน IEEE 754 ใช้ค่า bias เท่ากับ 127
130 - 127 = 3
ดังนั้นเลขชี้กำลัง = 3 ซึ่งหมายถึง 2³
(*IEEE 754 ใช้ค่า bias เพื่อแสดงเลขชี้กำลัง สำหรับความแม่นยำเดี่ยว (32 บิต) เลขชี้กำลังมี 8 บิต โดย bias คำนวณจาก: Bias = 2⁸⁻¹ − 1 = 127)
• เศษส่วน (M): 11100000000000000000000
ตามมาตรฐาน IEEE 754 เศษส่วนใช้รูปแบบปกติ "1 + ค่าทศนิยม" ดังนั้นค่าที่แท้จริงคือ: 1.11100000000000000000000₂
Convert to decimal:
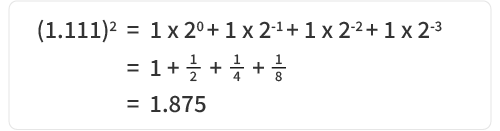
IEEE754 floating-point format is defined as:
ค่า = (−1)sign × 2exponent × (1 + fraction)
= (−1)0 × 23 × (1 + 0.875)
= 15
4. การเข้าถึงและแปลงข้อมูล Floating-Point ของ Modbus
ในการสื่อสารแบบ Modbus ข้อมูลจะถูกจัดเก็บไว้ในรีจิสเตอร์ โดยแต่ละรีจิสเตอร์มีความกว้าง 16 บิต อย่างไรก็ตาม การเก็บค่าตัวเลขแบบ floating-point แบบ single-precision ต้องใช้ 32 บิต ดังนั้นข้อมูลที่เกิน 16 บิตจะต้องครอบคลุมหลายรีจิสเตอร์ติดต่อกัน ซึ่งหมายความว่า float 32 บิตต้องใช้รีจิสเตอร์ติดกันสองช่อง
โปรโตคอล Modbus ระบุให้ใช้รูปแบบ Big-Endian สำหรับการส่งค่าที่มีหลายไบต์ ในรูปแบบ Big-Endian ไบต์ที่มีค่าสำคัญมากที่สุดจะถูกส่งก่อน ตัวอย่างเช่น ค่าเลขฐานสิบหก 16 บิต 0x1234 จะถูกส่งเป็น 0x12 ตามด้วย 0x34 บนบัส (Modbus Organization, 2006)
[4]
1 ) Modbus เก็บค่า Floating-Point 32 บิตอย่างไร
เลขทศนิยมลอยตัว 84.0 ถูกจัดเก็บใน Modbus อย่างไร?
• แปลงให้อยู่ในรูปแบบ IEEE 754 single-precision floating-point:
การแทนเลขฐานสองแบบ IEEE 754 single-precision (32 บิต) ของ 85.625 คือ:
01000010101010000000000000000000₂
• แปลงเป็นเลขฐานสิบหก: 0x42A80000
• การจัดเก็บใน Modbus (รูปแบบ Big-Endian):
เนื่องจากแต่ละรีจิสเตอร์ของ Modbus มีขนาด 16 บิต ค่าทศนิยม 32 บิตจึงถูกแบ่งเก็บใน 2 รีจิสเตอร์:
รีจิสเตอร์สูง (16 บิตแรก): 0x42A8
รีจิสเตอร์ต่ำ (16 บิตหลัง): 0x0000
2 ) วิธีถอดรหัสค่าจาก Modbus กลับเป็น Floating-Point
ตัวอย่าง:
ที่อยู่ของอุปกรณ์ (Slave ID): 0x01
รหัสฟังก์ชัน: 0x03 (อ่าน Holding Registers)
ที่อยู่รีจิสเตอร์เริ่มต้น: 0x1000
จำนวนรีจิสเตอร์ที่ต้องการอ่าน: 0x0002 (เพราะ float 32 บิตใช้ 2 รีจิสเตอร์)
➤ คำขอส่งผ่าน Modbus (TX - Master ส่งข้อมูล):
01 03 10 00 00 02 C5 CD
| ไบต์ |
คำอธิบาย |
ค่า
|
| 01 |
ที่อยู่ของอุปกรณ์ (Slave ID) |
0x01 |
| 03 |
รหัสฟังก์ชัน (อ่าน Holding Registers) |
0x03 |
| 10 00 |
ที่อยู่เริ่มต้น (0x1000) |
0x1000 |
| 00 02 |
จำนวนรีจิสเตอร์ (อ่าน 2 ช่อง) |
0x0002 |
| C5 CD |
ค่า CRC-16
|
0xC5CD |
➤ Modbus Device Response (RX - Slave responds):
01 03 04 42 A8 00 00 79 32
| ไบต์ |
คำอธิบาย |
ค่า |
| 01 |
ที่อยู่ของอุปกรณ์ (Slave ID) |
0x01 |
| 03 |
รหัสฟังก์ชัน (อ่าน Holding Registers) |
0x03 |
| 04 |
จำนวนไบต์ |
0x04 (4 bytes = 32-bit) |
| 42 A8 |
ค่าจากรีจิสเตอร์สูง
|
0x42A8 |
| 00 00 |
ค่าจากรีจิสเตอร์ต่ำ |
0x0000 |
| 79 32 |
ค่า CRC-16 |
0x7932 |
จากข้อมูลจะเห็นว่าค่าที่รวมกันคือ:
รีจิสเตอร์สูง = 0x42A8, รีจิสเตอร์ต่ำ = 0x0000
รวมเป็นค่าทั้งหมดแบบ 32 บิต (Big-Endian): 0x42A80000
รูปแบบเลขฐานสอง: 0100 0010 1010 1000 0000 0000 0000 0000
การถอดรหัสตาม IEEE 754:
• บิตเครื่องหมาย (S) = 0 (ค่าบวก)
• เลขชี้กำลัง (E) = 10000101₂ = 133
• เศษส่วน (M) = 01010000000000000000000₂
นำไปใช้ในสูตร IEEE 754 จะได้ค่าทศนิยม:
84.0
