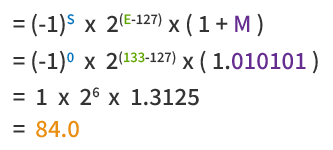Apa Itu Angka Floating-Point?
Angka floating-point atau aritmetika titik kambang adalah cara untuk merepresentasikan angka desimal atau angka yang sangat besar menggunakan memori yang terbatas. Seperti yang dijelaskan oleh Mitra (2017, para. 2), “Meski operasi bilangan bulat lebih cepat dan bebas dari kesalahan pembulatan, tipe integer tidak cocok untuk mewakili pecahan atau nilai dengan rentang yang sangat luas.”
Di sinilah angka floating-point berperan—mereka memungkinkan kita menangani data numerik yang bersifat kontinu secara lebih efisien. Tipe data ini sangat berguna dalam perhitungan ilmiah, seperti untuk merepresentasikan konstanta fisika atau mengukur jarak pada skala atom maupun galaksi. Nilai-nilai seperti ini sulit, bahkan mustahil, diwakili hanya dengan angka bulat.
Itulah sebabnya hampir semua bahasa pemrograman modern menyediakan dukungan untuk tipe data floating-point secara bawaan.
[1]
2. Representasi Floating-Point
Angka floating-point bekerja mirip dengan notasi ilmiah.
Sebagai contoh, angka 12345 dalam notasi ilmiah ditulis sebagai:
1.2345 × 10⁴
Di sini, 1.2345 disebut pecahan (atau mantissa), dan 4 adalah eksponen.
Notasi ilmiah menggunakan basis 10 (desimal), sementara angka floating-point menggunakan basis 2 (biner).
Ambil angka 15 sebagai contoh:
| Bilangan Bulat (Desimal) |
Notasi Ilmiah (Desimal) |
Floating-Point (Biner) |
| 15 |
(1,5)10 × 101 |
(1.111)2 × 23 |
Contoh: Merepresentasikan Angka 15 sebagai Nilai Floating-Point
Langkah 1: Ubah 15 ke dalam bentuk biner
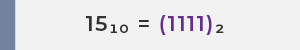
Langkah 2: Geser semua digit signifikan mantissa ke kanan tanda desimal hingga membentuk format (1.XXXX)₂ × 2ⁿ
Geser tanda desimal tiga posisi ke kiri. Untuk menjaga nilai tetap sama, pangkatkan basis 2 dengan angka 3
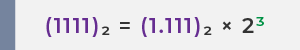
✅ Hasil Akhir Representasi Floating-Point :
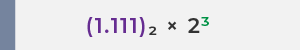
1 ) Format Floating-Point IEEE 754
Untuk menghindari hasil floating-point yang tidak konsisten di berbagai platform, IEEE (Institute of Electrical and Electronics Engineers) memperkenalkan standar IEEE 754 pada tahun 1985. Sejak tahun 1990-an, standar ini telah digunakan secara luas untuk menentukan cara representasi dan perhitungan angka floating-point (Wikipedia, 2024):
IEEE 754 mengatur:
- Format penyimpanan angka floating-point (misalnya, 32-bit Float32 dan 64-bit Float64).
- Aturan operasi floating-point (seperti mode pembulatan, nilai khusus seperti NaN dan infinity).
- Penanganan kasus khusus (misalnya overflow, underflow, dan pembagian dengan nol).
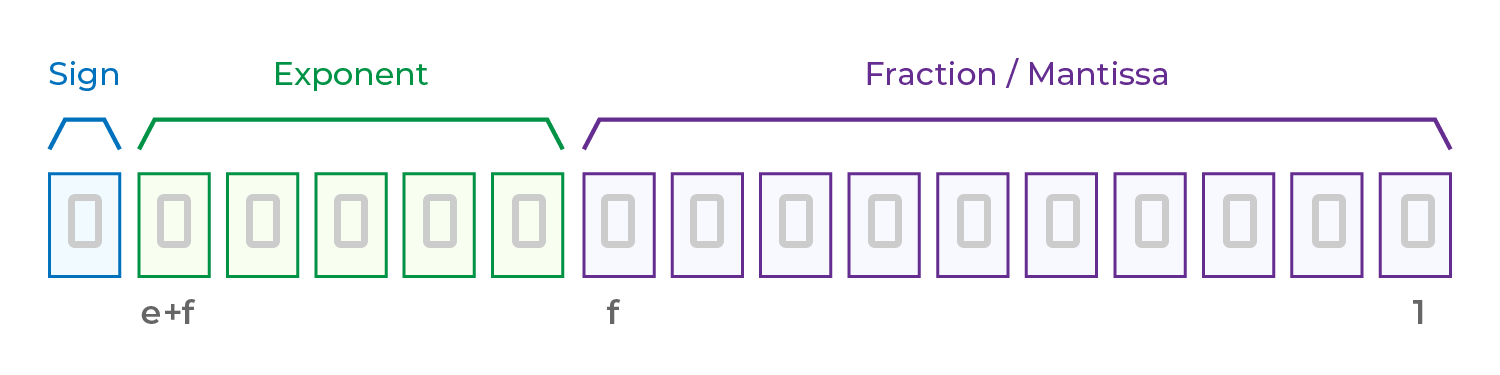
Struktur angka floating-point menurut IEEE 754 ditulis sebagai berikut:
Nilai = (−1)sign × 2eksponen × (1 + Mantissa)
Bit Tanda (Sign Bit): 1 bit, menentukan apakah angka bernilai positif atau negatif: 0 = positif / 1 = negatif
Bias Eksponen (Exponent Bias): Digunakan untuk mengatur jangkauan nilai (dalam pangkat 2), dihitung sebagai eksponen dikurangi nilai bias.
Bagian pecahan (mantisa): Mewakili nilai "1 + bagian desimal" dan menyimpan digit signifikan (mirip dengan format "1.XX" dalam notasi ilmiah).
2) Presisi Floating-Point: Float32 & Float64
Representasi floating-point dari
15 adalah
(1.111)₂ × 2³, yang ditulis sebagai:
(−1)⁰ × 2³ × (1.111)₂
Format ini mengikuti standar IEEE 754 dalam bentuk ternormalisasi. Saat komputer menyimpan angka floating-point, nilainya akan dikodekan mengikuti standar IEEE 754, baik dalam bentuk presisi tunggal (Float32) maupun presisi ganda (Float64).
Single Precision
Saat menyimpan angka floating-point, angka 1 di depan bersifat implisit (tidak perlu disertakan), sehingga hanya bagian pecahan yang disimpan, bukan keseluruhan bagian signifikan
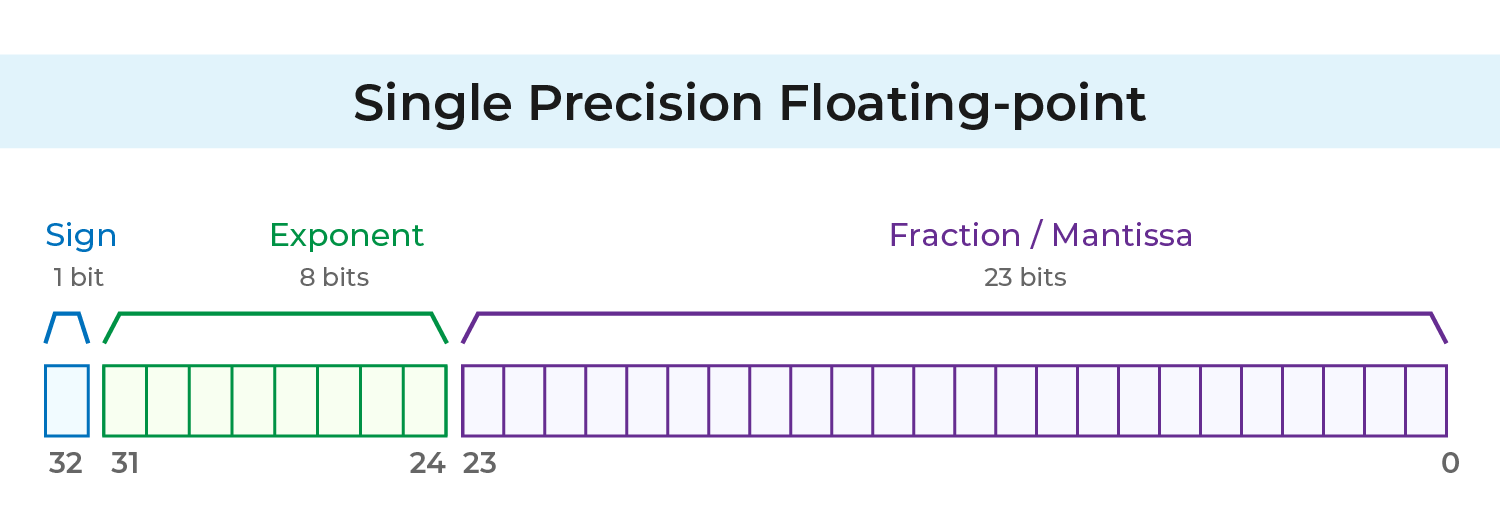
IEEE 754 presisi tunggal (Single Precision) menggunakan total 32 bit:
1 bit: Sign Bit
8 bit: Eksponen (m)
23 bit: Pecahan (f)
Pada presisi tunggal, eksponen diberi bias sebesar 127 untuk menghindari penyimpanan tanda negatif. Komputer menyimpan
m + 127 bukannya
m. Oleh karena itu, nilai eksponen maksimum adalah 127, dan nilai minimum adalah −126.
(Grainger College of Engineering, 2019)
*Untuk contoh perhitungan, silakan merujuk ke bagian berikutnya.
Double Precision
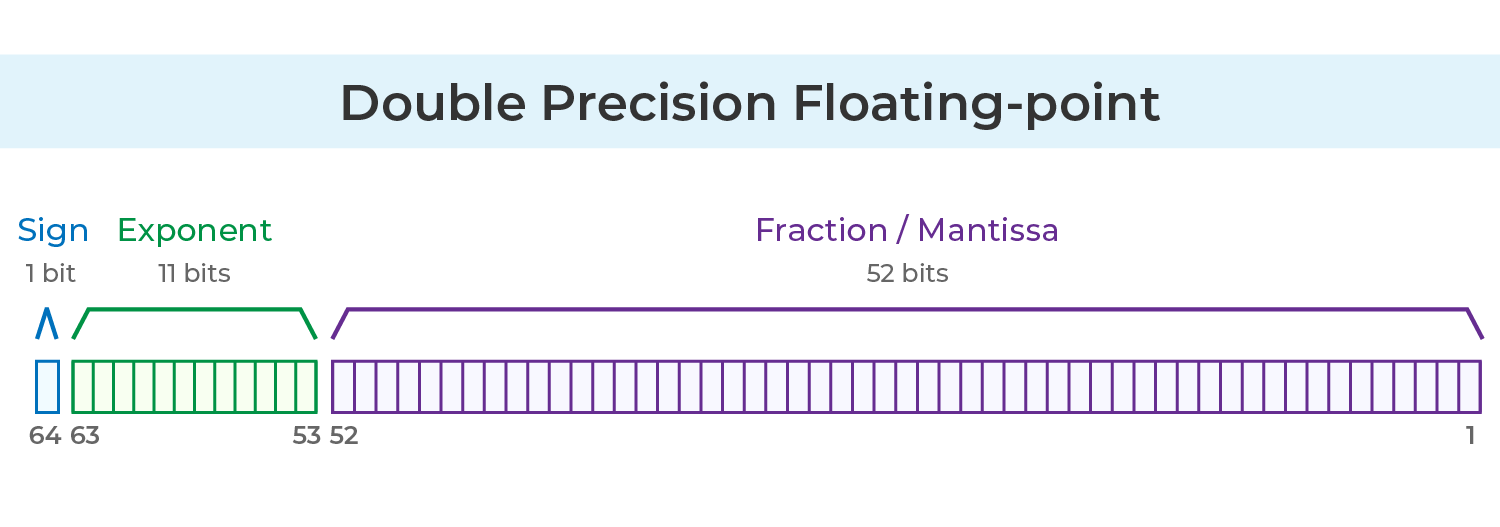
IEEE 754 presisi ganda (Double Precision) menggunakan total 64 bit:
1 bit: Sign Bit
11 bit: Eksponen (m)
52 bit: Bagian Pecahan (f)
Pada presisi ganda, eksponen diberi bias sebesar 1023 untuk menghindari penyimpanan tanda negatif. Komputer menyimpan
m + 1023 bukannya
m. Oleh karena itu, nilai eksponen maksimum adalah 1023, dan nilai minimum adalah −1022.
(Grainger College of Engineering, 2019)
Perbandingan Float32 dan Float64
| Fitur |
Float32 (Single Precision) |
Float64 (Double Precision) |
| Panjang Bit |
32 bit |
64 bit |
| Panjang Pecahan |
23 bit (sekitar 7–8 digit desimal) |
52 bit (sekitar 15–16 digit desimal) |
| Panjang Eksponen |
8 bit (bias: 127) |
11 bit (bias: 1023) |
| Rentang Nilai |
Aprox. 10⁻³⁸ ~ 10³⁸ |
Aprox. 10⁻³⁸ ~ 10³⁸ |
| Pemakaian Memori |
4 byte (32-bit) |
8 byte (64-bit) |
| Kinerja |
Lebih cepat (ideal untuk pemrosesan grafis, pelatihan AI) |
Lebih lambat namun lebih akurat (lebih baik untuk komputasi ilmiah) |
| Aplikasi Umum |
• Pengembangan game, pemrosesan grafis (komputasi GPU)
• Pembelajaran mesin (misalnya, presisi campuran dalam TensorFlow)
• Dataset besar dengan kebutuhan presisi rendah |
• Komputasi ilmiah dan simulasi (misalnya, peramalan cuaca, pemodelan fisika)
• Perhitungan finansial (untuk menghindari kesalahan pembulatan)
• Komputasi numerik presisi tinggi (misalnya, aplikasi rekayasa) |
3. Contoh Perhitungan Floating-Point 32-bit (Single Precision)
| Format Single Precision (Float32, 32-bit) |
| Komponen |
Panjang Bit |
Deskripsi |
| Bit Tanda (S) |
1 bit |
0 (positif) |
| Eksponen (E) |
8 bit |
3 + 127 = 130 = 10000010₂ |
| Pecahan (M) |
23 bit |
11100000000000000000000 (hilangkan 1 di depan, simpan hanya 111) |
| Penyimpanan |
32 bit |
0 10000010 11100000000000000000000 |
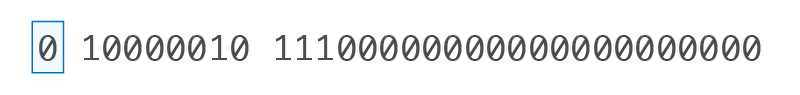• Bit Tanda (S): 0
(−1)⁰ = 1 (menunjukkan angka positif)
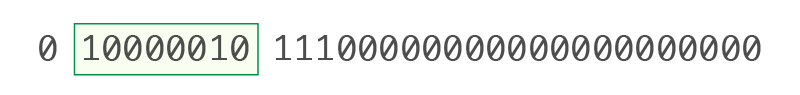• Eksponen (E) (Bit 2–9): 10000010
Konversi ke desimal: 10000010₂ = 130₁₀
*IEEE 754 menggunakan nilai bias 127
130 - 127 = 3
Jadi, eksponen = 3, berarti 2³
(*IEEE 754 menggunakan bias untuk merepresentasikan eksponen. Untuk presisi tunggal (32-bit), bidang eksponen menggunakan 8 bit. Menurut definisi IEEE 754, bias dihitung sebagai: Bias = 2⁸⁻¹ – 1 = 127)
• Pecahan (M): 11100000000000000000000
Menurut IEEE 754, pecahan menggunakan bentuk normalisasi “1 + nilai pecahan,” sehingga nilai sebenarnya adalah: 1.11100000000000000000000₂
Konversi ke desimal: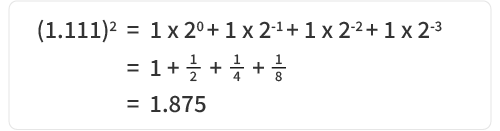 
Format floating-point IEEE754 didefinisikan sebagai:
Nilai = (−1)sign × 2eksponen × (1 + Mantisa)
= (−1)0 × 23 × (1 + 0.875)
= 15
4. Akses dan Konversi Floating-Point Modbus
Dalam komunikasi Modbus, data disimpan dalam register, dengan setiap register memiliki lebar 16 bit. Namun, untuk merepresentasikan angka floating-point presisi tunggal, diperlukan 32 bit. Untuk menangani hal ini dalam arsitektur Modbus, data yang melebihi 16 bit harus tersebar di beberapa alamat register berturut-turut. Oleh karena itu, sebuah float 32-bit perlu memanfaatkan dua register yang berdekatan.
Protokol Modbus menspesifikasikan penggunaan format Big-Endian untuk mentransmisikan nilai multi-byte. Dalam urutan Big-Endian, byte yang paling signifikan dikirim terlebih dahulu. Sebagai contoh, nilai hexadecimal 16-bit 0x1234 akan dikirimkan di bus sebagai 0x12 diikuti oleh 0x34. (Modbus Organization, 2006)
[4]
1) Cara Modbus Menyimpan Angka Floating-Point 32-bit
Bagaimana angka floating-point 84.0 disimpan dalam Modbus?
• Konversi ke format floating-point presisi tunggal IEEE 754:
Representasi biner IEEE 754 presisi tunggal (32-bit) untuk 85.625 adalah:
01000010101010000000000000000000₂
• Konversi ke format heksadesimal: 0x42A80000
• Penyimpanan dalam Modbus (format Big-Endian):
Karena setiap register Modbus adalah 16 bit, angka floating-point 32-bit dibagi menjadi dua register:
Register tinggi (16 bit pertama): 0x42A8
Register rendah (16 bit terakhir): 0x0000
2) Cara Mendekode Nilai Modbus Kembali Menjadi Angka Floating-Point
Contoh:
Alamat Perangkat (Slave ID): 0x01
Kode Fungsi: 0x03 (Baca Holding Registers)
Alamat Register Awal: 0x1000
Jumlah Register yang Dibaca: 0x0002 (karena angka floating-point 32-bit memerlukan dua register 16-bit)
➤ **Permintaan Transmisi Modbus (TX - Master mengirim data):**
01 03 10 00 00 02 C5 CD
| Byte |
Deskripsi |
Nilai |
| 01 |
Alamat Perangkat (Slave ID) |
0x01 |
| 03 |
Kode Fungsi (Baca Holding Registers) |
0x03 |
| 10 00 |
Alamat Awal (0x1000) |
0x1000 |
| 00 02 |
Jumlah Register (Baca 2) |
0x0002 |
| C5 CD |
Checksum CRC-16 |
0xC5CD |
➤ **Respon Perangkat Modbus (RX - Slave merespon):**
01 03 04 42 A8 00 00 79 32
| Byte |
Deskripsi |
Nilai |
| 01 |
Alamat Perangkat (Slave ID) |
0x01 |
| 03 |
Kode Fungsi (Baca Holding Registers) |
0x03 |
| 04 |
Jumlah Byte |
0x04 (4 byte = 32-bit) |
| 42 A8 |
Nilai Register Tinggi |
0x42A8 |
| 00 00 |
Nilai Register Rendah |
0x0000 |
| 79 32 |
Checksum CRC-16 |
0x7932 |
Seperti yang ditunjukkan, data register yang digabungkan adalah:
Register 16-bit Tinggi = 0x42A8, Register 16-bit Rendah = 0x0000
Digabungkan menjadi nilai 32-bit (Big-Endian default): 0x42A80000
Representasi biner: 0100 0010 1010 1000 0000 0000 0000 0000
Dekonstruksi IEEE 754:
• Bit tanda (S) = 0 (positif)
• Eksponen (E) = 10000101₂ = 133
• Fraksi (M) = 01010000000000000000000₂
Masukkan ke dalam rumus IEEE 754 untuk mendapatkan nilai desimal:
84.0
