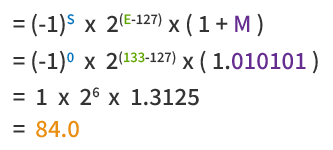1. 부동소수점 숫자란?
부동소수점 숫자는 제한된 메모리 공간에서 소수 또는 매우 큰 숫자를 표현하기 위한 방법입니다. Mitra (2017, para. 2)에 따르면, “정수 연산은 더 빠르고 반올림 오류가 없지만, 정수형은 분수나 아주 큰 범위의 값을 표현하는 데 적합하지 않다”고 합니다.
이럴 때 부동소수점 숫자가 유용합니다. 연속적인 수치 데이터를 보다 효과적으로 처리할 수 있도록 해주며, 물리 상수나 원자 단위 또는 은하 단위 거리 측정 등 과학적 계산에 특히 유용합니다. 이러한 값들은 정수로 표현하기 어렵거나 불가능하기 때문에, 대부분의 현대 프로그래밍 언어는 부동소수점 데이터 타입을 기본으로 지원합니다.
[1]
2. 부동소수점 표현 방식
부동소수점 숫자는 과학적 표기법과 유사한 방식으로 작동합니다.
예를 들어, 숫자 12345 는 과학적 표기법으로 다음과 같이 표현됩니다:
1.2345 × 10⁴
여기서 1.2345 는 가수(mantissa), 4 는 지수(exponent) 라고 합니다.
과학적 표기법은 10진수를 사용하지만, 부동소수점은 2진수를 사용합니다.
예를 들어 숫자 15는 다음과 같이 표현됩니다:
| 정수 (10진수) |
과학적 표기 (10진수) |
부동소수점 (2진수) |
| 15 |
(1.5)10 × 101 |
(1.111)2 × 23 |
예시: 숫자 15를 부동소수점 값으로 표현하기
1 단계: 15 를 이진수로 변환
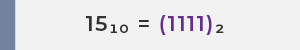
2 단계: 가수의 유효 숫자를 소수점 오른쪽으로 이동하여 (1.XXXX)₂ × 2ⁿ 형태로 만듭니다.
소수점을 왼쪽으로 세 칸 이동하면 값을 유지하기 위해 밑수 2를 3제곱해야 합니다.
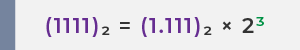
✅ 숫자 15 의 부동소수점 표현은
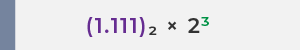
1 ) IEEE 754 부동소수점 형식
서로 다른 플랫폼 간의 부동소수점 계산 결과가 일관되지 않게 나오는 것을 방지하기 위해, IEEE(전기전자기술자협회)는 1985년에 IEEE 754 표준을 제정하였으며, 1990년대부터 널리 채택되었습니다. 이 표준은 부동소수점 숫자의 표현 및 계산 방식을 정의합니다 (Wikipedia, 2024):
IEEE 754는 다음을 정의합니다:
- 부동소수점 숫자의 저장 형식 (예: 32비트 Float32, 64비트 Float64)
- 부동소수점 연산 규칙 (예: 반올림 모드, NaN 및 무한대 같은 특수값)
- 예외 처리 사례 (예: 오버플로우, 언더플로우, 0으로 나누기)
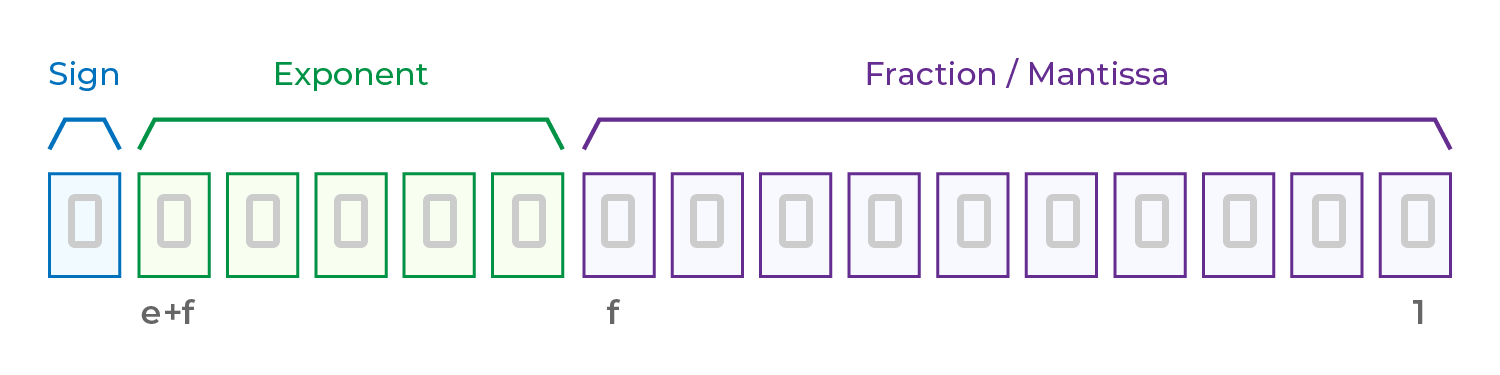
IEEE 754 는 부동소수점 숫자의 구조를 다음과 같이 정의합니다:
값 = (−1)부호 × 2지수 × (1 + 가수)
부호 비트: 1비트, 숫자가 양수인지 음수인지 결정함 (0 = 양수 / 1 = 음수)
지수 바이어스: 2의 거듭제곱 형태로 범위를 조절하며, 저장 시에는 (지수 + 바이어스)로 저장됨
가수(Mantissa): “1 + 소수 부분”을 표현하며, 중요한 숫자(유효 숫자)를 저장함 (과학적 표기법의 “1.XX”와 유사)
2 ) 부동소수점 정밀도: Float32 및 Float64
15 의 부동소수점 표현은
(1.111)₂ × 2³ 이며, 다음과 같이 표기됩니다:
(−1)⁰ × 2³ × (1.111)₂
이는 IEEE 754 정규화된 형식을 따릅니다.
컴퓨터가 부동소수점 숫자를 저장할 때는 IEEE 754 표준에 따라 단정밀도 (Float32) 또는 배정밀도(Float64) 형식을 사용합니다.
단정밀도 (Single Precision)
부동소수점을 저장할 때는 가장 앞의 1은 기본적으로 생략됩니다. 따라서 가수 전체가 아닌 소수점 이하 부분만 저장됩니다.
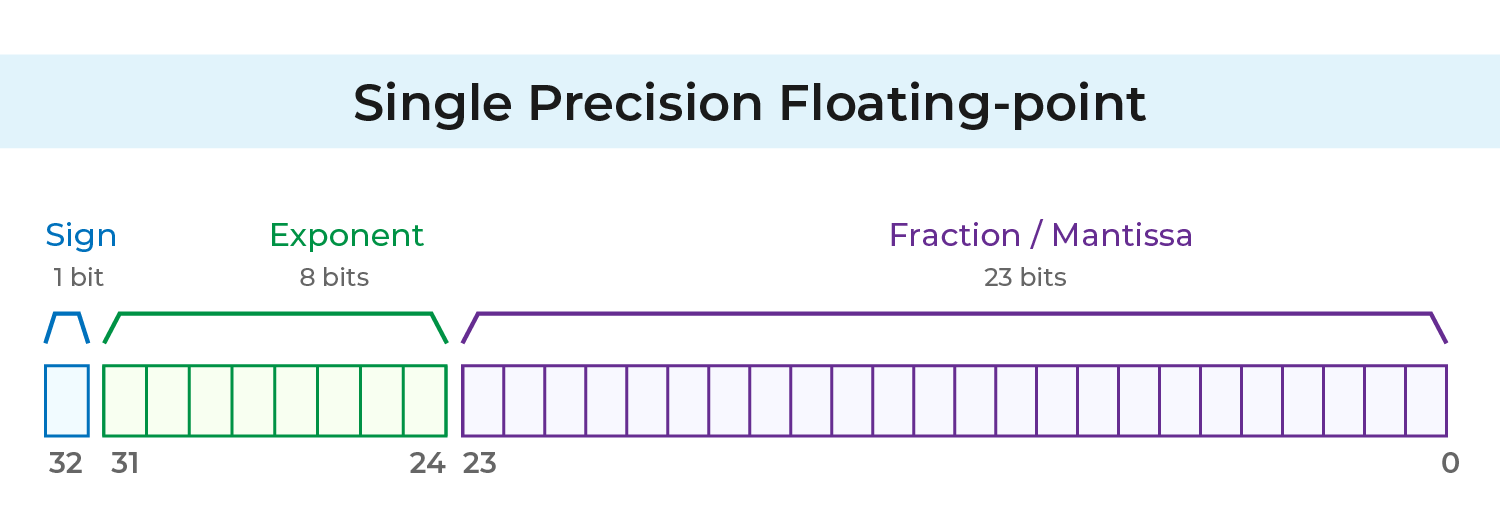
IEEE 754 단정밀도는 총 32비트를 사용합니다:
1 비트: 부호 비트
8 비트: 지수 (m)
23 비트: 가수 (f)
단정밀도에서는 음수를 저장하지 않기 위해 지수에 127을 더한 값을 저장합니다. 즉, 컴퓨터는 실제 지수
m 대신
m + 127 을 저장합니다. 따라서 지수의 최대값은 127이고, 최소값은 −126입니다.
(Grainger College of Engineering, 2019)
* 계산 예시는 다음 섹션을 참조하세요.
배정밀도 (Double Precision)
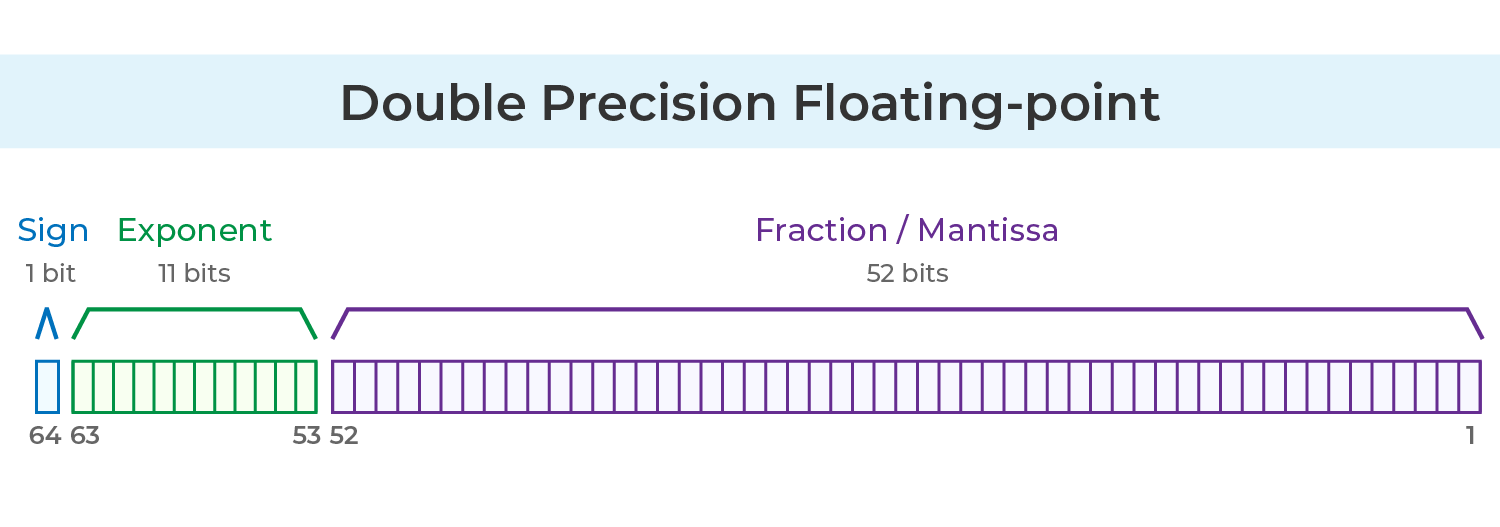
IEEE 754 배정밀도는 총 64 비트를 사용합니다:
1 비트: 부호 비트
11 비트: 지수 (m)
52 비트: 가수 (f)
배정밀도에서는 음수를 저장하지 않기 위해 지수에 1023을 더한 값을 저장합니다. 즉, 컴퓨터는 실제 지수
m 대신
m + 1023 을 저장합니다. 따라서 지수의 최대값은 1023이고, 최소값은 −1022입니다.
(Grainger College of Engineering, 2019)
Float32 vs Float64 기능 비교
| 항목 |
Float32 (단정밀도) |
Float32 (단정밀도) |
| 비트 길이 |
32 비트 |
64 비트 |
| 가수 길이 |
23 비트 (약 7~8자리 소수) |
52 비트 (약 15~16자리 소수) |
| 지수 길이 |
8 비트 (바이어스: 127) |
11 비트 (바이어스: 1023)
|
| 값의 범위 |
약 10⁻³⁸ ~ 10³⁸ |
약 10⁻³⁰⁸ ~ 10³⁰⁸ |
| 메모리 사용량 |
4바이트 (32비트) |
8 바이트 (64비트) |
| 성능 |
빠름 (그래픽 처리, AI 학습에 적합) |
느리지만 정확도 높음 (과학 계산에 적합) |
| 주요 용도 |
• 게임 개발, 그래픽 처리 (GPU 컴퓨팅)
• 머신러닝 (예: TensorFlow 혼합 정밀도)
• 정밀도가 낮아도 되는 대용량 데이터 처리 |
• 과학 계산 및 시뮬레이션 (예: 기상 예측, 물리 시뮬레이션)
• 금융 계산 (반올림 오류 방지 목적)
• 고정밀 수치 계산 (예: 공학 분야 응용) |
3. 32 비트 부동소수점 계산 예시
| 단정밀도 (Float32, 32비트) 형식 |
| 구성 요소 |
비트 길이 |
설명 |
| 부호 비트 (S) |
1 비트 |
0 (양수) |
| 지수 (E) |
8 비트 |
3 + 127 = 130 = 10000010₂ |
| 가수 (M) |
23 비트 |
11100000000000000000000 (선행 1.은 생략하고 111만 저장) |
| 저장 값 |
32 비트 |
0 10000010 11100000000000000000000 |
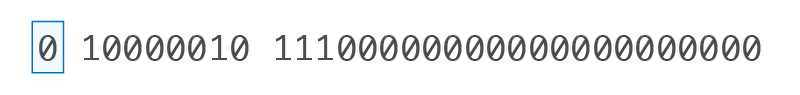• 부호 비트 (S): 0
(−1)⁰ = 1 (양수를 의미함)
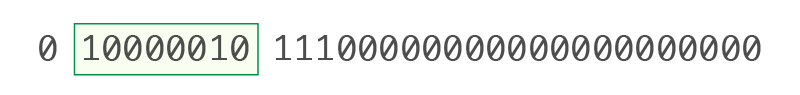• 지수 (E) (비트 2~9): 10000010
10진수로 변환: 10000010₂ = 130₁₀
*IEEE 754는 바이어스 값으로 127을 사용
130 - 127 = 3
따라서 지수 = 3 → 23
(*IEEE 754는 지수를 바이어스 방식으로 표현함. 단정밀도(32비트)의 경우 지수는 8비트를 사용하며, 바이어스는 Bias = 2⁸⁻¹ − 1 = 127로 정의됨)
• 가수 (M): 11100000000000000000000
IEEE 754에 따르면, 가수는 정규화 형태인 “1 + 소수값”으로 해석되며, 실제 값은: 1.11100000000000000000000₂
십진수로 변환:
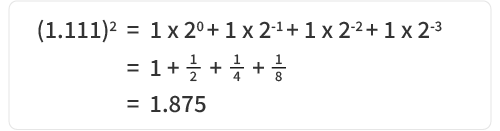
IEEE754 부동소수점 형식은 다음과 같이 정의됩니다::
값 = (−1)부호 × 2지수 × (1 + 가수)
= (−1)0 × 23 × (1 + 0.875)
= 15
4. Modbus 부동소수점 접근 및 변환
Modbus 통신에서는 데이터가 16비트 너비의 레지스터에 저장됩니다. 그러나 단정밀도 부동소수점 숫자는 32비트를 필요로 하기 때문에, 16비트를 초과하는 데이터는 여러 개의 연속된 레지스터 주소에 나뉘어 저장되어야 합니다.
Modbus 프로토콜은 멀티 바이트 값을 전송할 때 Big-Endian 형식을 사용하도록 규정합니다. Big-Endian 순서에서는 가장 상위 바이트(MSB)가 먼저 전송됩니다. 예를 들어, 16비트 값 0x1234는 버스 상에서 0x12 → 0x34 순으로 전송됩니다. (Modbus Organization, 2006)
[4]
1 ) Modbus 에서 32비트 부동소수점 숫자를 저장하는 방식
Modbus에서 부동소수점 숫자 84.0은 어떻게 저장될까요?
• IEEE 754 단정밀도 부동소수점 형식으로 변환:
숫자 85.625 의 IEEE 754 단정밀도(32비트) 이진 표현은:
01000010101010000000000000000000₂
• 16진수로 변환: 0x42A80000
• Modbus 저장 방식 (Big-Endian 순서):
Modbus 레지스터는 16비트 단위이므로, 32비트 부동소수점 값은 두 개의 연속된 레지스터에 나뉘어 저장됩니다:
상위 레지스터 (앞 16비트): 0x42A8
하위 레지스터 (뒤 16비트): 0x0000
2 ) Modbus 값을 다시 부동소수점으로 해석하는 방법
예시:
디바이스 주소 (Slave ID): 0x01
기능 코드: 0x03 (Holding Register 읽기)
시작 레지스터 주소: 0x1000
읽을 레지스터 수: 0x0002 (32비트 부동소수점은 16비트 레지스터 2개를 차지하므로)
➤ Modbus 송신 요청 (TX - 마스터가 데이터 전송):
01 03 10 00 00 02 C5 CD
| 바이트 |
설명 |
값 |
| 01 |
디바이스 주소 (Slave ID) |
0x01 |
| 03 |
기능 코드 (Holding Register 읽기) |
0x03 |
| 10 00 |
시작 주소 (0x1000) |
0x1000 |
| 00 02 |
읽을 레지스터 수 (2개) |
0x0002 |
| C5 CD |
CRC-16 체크섬 |
0xC5CD |
➤ Modbus 디바이스 응답 (RX - 슬레이브 응답):
01 03 04 42 A8 00 00 79 32
| 바이트 |
설명 |
값
|
| 01 |
디바이스 주소 (Slave ID) |
0x01 |
| 03 |
기능 코드 (Holding Register 읽기) |
0x03 |
| 04 |
데이터 바이트 수 |
0x04 (4바이트 = 32비트) |
| 42 A8 |
상위 레지스터 값 |
0x42A8 |
| 00 00 |
하위 레지스터 값 |
0x0000 |
| 79 32 |
CRC-16 체크섬 |
0x7932 |
표시된 바와 같이, 결합된 레지스터 데이터는 다음과 같습니다:
상위 16비트 = 0x42A8, 하위 16비트 = 0x0000
기본 Big-Endian 순서로 결합된 32비트 값: 0x42A80000
이진 표현: 0100 0010 1010 1000 0000 0000 0000 0000
IEEE 754 분해 결과:
• 부호 비트 (S) = 0 (양수)
• 지수 (E) = 10000101₂ = 133
• 가수 (M) = 01010000000000000000000₂
IEEE 754 공식을 적용하여 10진수 값으로 환산하면:
84.0
