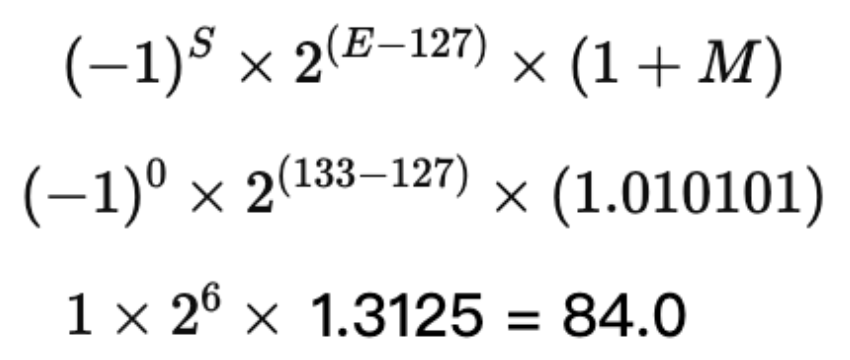1. Số dấu phẩy động là gì?
Một số dấu phẩy động là cách để biểu diễn các số thập phân hoặc các số rất lớn bằng cách sử dụng dung lượng bộ nhớ giới hạn. Như Mitra (2017, đoạn 2) đã chỉ ra: "Mặc dù các phép toán số nguyên nhanh hơn và không có lỗi làm tròn, nhưng kiểu dữ liệu số nguyên không phù hợp để biểu diễn các phân số hoặc giá trị trong phạm vi quá rộng."
Đó là lý do số dấu phẩy động được sử dụng — giúp xử lý dữ liệu số liên tục hiệu quả hơn. Chúng đặc biệt hữu ích trong các phép tính khoa học, như biểu diễn hằng số vật lý hoặc đo khoảng cách ở cấp độ nguyên tử hoặc thiên hà. Những giá trị này rất khó, nếu không muốn nói là không thể, biểu diễn bằng số nguyên. Vì thế, hầu hết các ngôn ngữ lập trình hiện đại đều hỗ trợ kiểu dữ liệu số dấu phẩy động như một tiêu chuẩn.
[1]
2. Biểu diễn số dấu phẩy động
Số dấu phẩy động hoạt động tương tự như ký hiệu khoa học. Ví dụ, số 12345 trong ký hiệu khoa học được viết là 1.2345 × 10⁴. Trong đó, 1.2345 là phần trị (hoặc mantissa), và 4 là số mũ. Ký hiệu khoa học sử dụng cơ số 10 (hệ thập phân), trong khi số dấu phẩy động sử dụng cơ số 2 (nhị phân). Lấy số 15 làm ví dụ:
| Số nguyên (thập phân) |
Ký hiệu khoa học (thập phân) |
Số dấu phẩy động (nhị phân) |
| 15 |
(1.5)10 × 101 |
(1.111)2 × 23 |
Ví dụ: Biểu diễn số 15 dưới dạng số dấu phẩy động
Bước 1: Chuyển 15 sang nhị phân
15₁₀ = (1111)₂
Bước 2: Dịch các chữ số có nghĩa của phần trị sang phải dấu phẩy để tạo thành (1.XXXX)₂ × 2ⁿ
Di chuyển dấu phẩy sang trái 3 vị trí. Để giữ nguyên giá trị, lũy thừa cơ số 2 lên 3
(1111)₂ = (1.111)₂ × 2³
Biểu diễn số dấu phẩy động của 15 là (1.111)₂ × 2³
1 ) Định dạng số dấu phẩy động IEEE 754
Để tránh sự không nhất quán trong kết quả số dấu phẩy động giữa các nền tảng khác nhau, IEEE (Viện Kỹ sư Điện và Điện tử) đã đưa ra chuẩn IEEE 754 vào năm 1985, và được áp dụng rộng rãi từ những năm 1990 để xác định cách biểu diễn và tính toán số dấu phẩy động (Wikipedia, 2024):
IEEE 754 quy định:
• Các định dạng lưu trữ số dấu phẩy động (ví dụ: 32-bit Float32 và 64-bit Float64).
• Quy tắc cho các phép toán dấu phẩy động (ví dụ: làm tròn, giá trị đặc biệt như NaN và vô cực).
• Các trường hợp ngoại lệ (ví dụ: tràn, hụt, chia cho 0).
IEEE 754 xác định cấu trúc của số dấu phẩy động như sau:
Giá trị = (−1)sign × 2exponent × (1 + fraction)
Bit dấu: 1 bit, xác định số là dương hay âm: 0 = dương / 1 = âm
Độ lệch số mũ: Dùng để điều chỉnh phạm vi giá trị (theo lũy thừa cơ số 2), được tính bằng số mũ trừ đi độ lệch.
Phần trị (Mantissa): Biểu thị "1 + phần thập phân" và lưu trữ các chữ số có nghĩa (giống như "1.XX" trong ký hiệu khoa học).
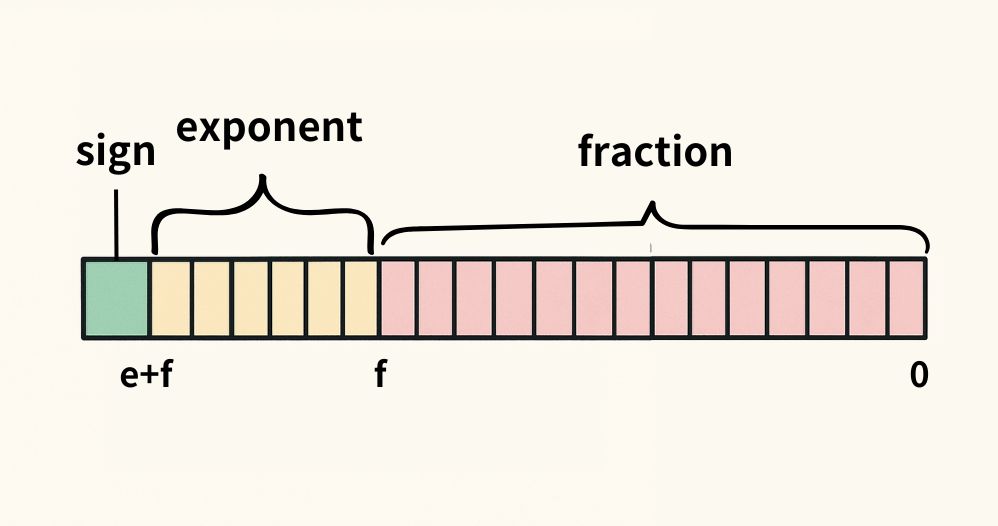
2 ) Độ chính xác của số dấu phẩy động: Float32 & Float64
Biểu diễn số dấu phẩy động của 15 là (1.111)₂ × 2³, được viết dưới dạng (−1)⁰ × 2³ × (1.111)₂. Đây là định dạng chuẩn hóa theo IEEE 754. Khi máy tính lưu trữ số dấu phẩy động, chúng mã hóa theo chuẩn IEEE 754 bằng cách sử dụng độ chính xác đơn (Float32) hoặc độ chính xác kép (Float64).
Độ chính xác đơn
Khi lưu trữ một số dấu phẩy động, số 1 đứng đầu được giả định sẵn. Do đó, chỉ phần thập phân (sau dấu phẩy) được lưu, không lưu toàn bộ phần trị.
Độ chính xác đơn
Khi lưu trữ một số dấu phẩy động, số 1 đứng đầu là ngầm định, nên chỉ lưu phần thập phân thay vì toàn bộ phần trị.
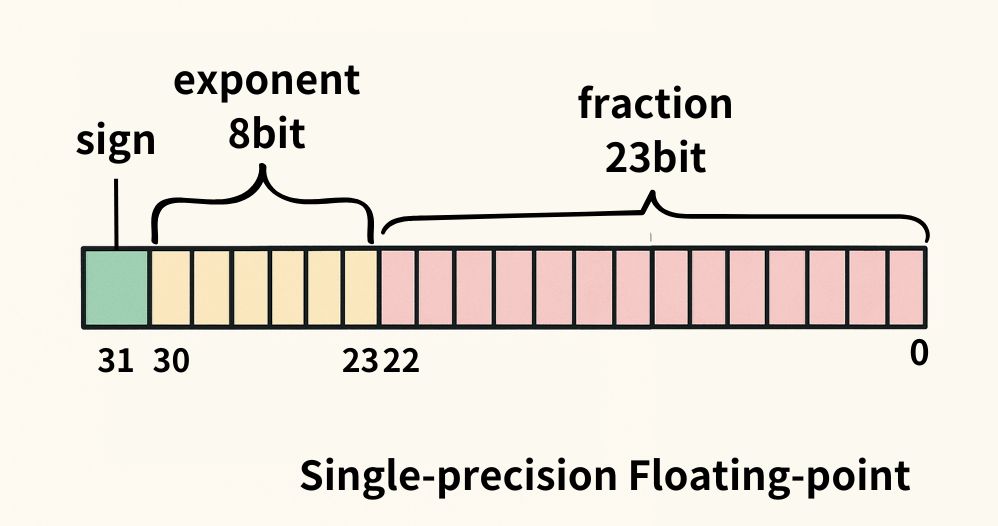
Định dạng đơn IEEE 754 sử dụng tổng cộng 32 bit:
1 bit: Bit dấu
8 bit: Số mũ (m)
23 bit: Phần trị (f)
Trong định dạng đơn, số mũ được lệch 127 để tránh lưu dấu âm. Máy tính lưu trữ m + 127 thay vì m. Vì vậy, giá trị số mũ tối đa là 127 và tối thiểu là −126. (Grainger College of Engineering, 2019)
* Ví dụ tính toán sẽ được trình bày ở phần sau.
Độ chính xác kép
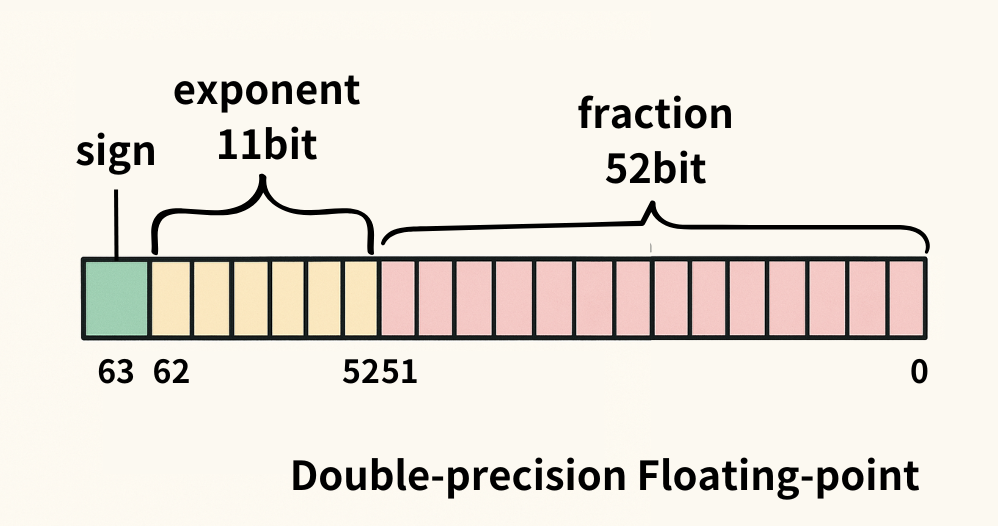
Định dạng IEEE 754 độ chính xác kép sử dụng tổng cộng 64 bit:
1 bit: Bit dấu
11 bit: Số mũ (m)
52 bit: Phần trị (f)
Trong độ chính xác kép, số mũ được lệch 1023 để tránh lưu dấu âm. Máy tính lưu trữ m + 1023 thay vì m. Do đó, giá trị số mũ tối đa là 1023 và tối thiểu là −1022. (Grainger College of Engineering, 2019)
So sánh đặc điểm giữa Float32 và Float64
| Đặc điểm |
Float32 (Độ chính xác đơn) |
Float64 (Độ chính xác kép) |
| Độ dài bit |
32 bit |
64 bit |
| Độ dài phần trị |
23 bit (khoảng 7–8 chữ số thập phân) |
52 bit (khoảng 15–16 chữ số thập phân) |
| Độ dài số mũ |
8 bit (độ lệch: 127) |
11 bit (độ lệch: 1023) |
| Phạm vi giá trị |
Xấp xỉ 10⁻³⁸ ~ 10³⁸ |
Xấp xỉ 10⁻³⁰⁸ ~ 10³⁰⁸ |
| Dung lượng bộ nhớ |
4 byte (32 bit) |
8 byte (64 bit) |
| Hiệu năng |
Nhanh hơn (lý tưởng cho xử lý đồ họa, huấn luyện AI) |
Chậm hơn nhưng chính xác hơn (tốt hơn cho tính toán khoa học) |
| Ứng dụng phổ biến |
• Phát triển trò chơi, xử lý đồ họa (GPU computing)
• Machine learning (ví dụ: mixed precision trong TensorFlow)
• Dữ liệu lớn với yêu cầu độ chính xác thấp
|
• Tính toán khoa học và mô phỏng (ví dụ: dự báo thời tiết, mô hình vật lý)
• Tính toán tài chính (để tránh lỗi làm tròn)
• Tính toán số có độ chính xác cao (ví dụ: ứng dụng kỹ thuật)
|
3. Ví dụ tính toán số dấu phẩy động 32 bit
| Định dạng Độ Chính Xác Đơn (Float32, 32 bit) |
| Thành phần |
Độ dài bit |
Mô tả |
| Bit dấu (S) |
1 bit |
0 (số dương) |
| Số mũ (E) |
8 bit |
3 + 127 = 130 = 10000010₂ |
| Phần trị (M) |
23 bit |
11100000000000000000000 (loại bỏ số 1. dẫn đầu, chỉ lưu 111) |
| Lưu trữ |
32 bit |
0 10000010 11100000000000000000000 |
 • Bit dấu (S): 0
• Bit dấu (S): 0
(−1)⁰ = 1 (biểu thị số dương)
 • Số mũ (E) (Bit 2–9): 10000010
• Số mũ (E) (Bit 2–9): 10000010
Chuyển sang thập phân: 10000010₂ = 130₁₀
*IEEE 754 sử dụng giá trị thiên vị là 127
130 - 127 = 3
Vậy nên, số mũ = 3, nghĩa là 2³
(*IEEE 754 sử dụng giá trị thiên vị để biểu diễn số mũ. Với độ chính xác đơn (32 bit), trường số mũ sử dụng 8 bit. Theo định nghĩa của IEEE 754, thiên vị được tính là: Bias = 2⁸⁻¹ − 1 = 127)
 • Phần trị (M): 11100000000000000000000
• Phần trị (M): 11100000000000000000000
Theo chuẩn IEEE 754, phần trị sử dụng dạng chuẩn hóa “1 + phần phân số”, nên giá trị thực tế là: 1.11100000000000000000000₂

4. Truy cập và chuyển đổi số dấu phẩy động trong Modbus
Trong giao tiếp Modbus, dữ liệu được lưu trữ trong các thanh ghi, mỗi thanh ghi có độ rộng 16 bit. Tuy nhiên, để biểu diễn một số dấu phẩy động độ chính xác đơn cần 32 bit. Để xử lý điều này trong kiến trúc Modbus, dữ liệu vượt quá 16 bit phải trải qua nhiều địa chỉ thanh ghi liên tiếp. Do đó, một số dấu phẩy động 32 bit cần chiếm hai thanh ghi liền kề.
Giao thức Modbus quy định sử dụng định dạng Big-Endian để truyền các giá trị nhiều byte. Trong thứ tự Big-Endian, byte quan trọng nhất được gửi trước. Ví dụ, giá trị hex 16 bit 0x1234 sẽ được truyền trên bus dưới dạng 0x12 sau đó là 0x34. (Modbus Organization, 2006)
[4]
1 ) Modbus lưu trữ số dấu phẩy động 32 bit như thế nào
Số dấu phẩy động 84.0 được lưu trữ trong Modbus như thế nào?
• Chuyển đổi sang định dạng số dấu phẩy động độ chính xác đơn IEEE 754:
Biểu diễn nhị phân IEEE 754 (32 bit) của 85.625 là: 01000010101010000000000000000000₂
• Chuyển sang hệ thập lục phân: 0x42A80000
• Lưu trữ trong Modbus (định dạng Big-Endian):
Vì mỗi thanh ghi Modbus có 16 bit, nên một số dấu phẩy động 32 bit sẽ được chia thành hai thanh ghi:
Thanh ghi cao (16 bit đầu): 0x42A8
Thanh ghi thấp (16 bit sau): 0x0000
2 ) Cách giải mã giá trị Modbus thành số dấu phẩy động
Ví dụ:
Địa chỉ thiết bị (Slave ID): 0x01
Mã chức năng: 0x03 (Đọc thanh ghi giữ)
Địa chỉ thanh ghi bắt đầu: 0x1000
Số lượng thanh ghi cần đọc: 0x0002 (vì số dấu phẩy động 32 bit chiếm hai thanh ghi 16 bit)
➤ Yêu cầu truyền Modbus (TX - Bộ điều khiển gửi dữ liệu):
01 03 10 00 00 02 C5 CD
| Byte |
Mô tả |
Giá trị |
| 01 |
Địa chỉ thiết bị (Slave ID) |
0x01 |
| 03 |
Mã chức năng (Đọc thanh ghi giữ) |
0x03 |
| 10 00 |
Địa chỉ bắt đầu (0x1000) |
0x1000 |
| 00 02 |
Số lượng thanh ghi (Đọc 2) |
0x0002 |
| C5 CD |
Mã kiểm tra CRC-16 |
0xC5CD |
➤ Phản hồi từ thiết bị Modbus (RX - Slave phản hồi):
01 03 04 42 A8 00 00 79 32
| Byte |
Mô tả |
Giá trị |
| 01 |
Địa chỉ thiết bị (Slave ID) |
0x01 |
| 03 |
Mã chức năng (Đọc thanh ghi giữ) |
0x03 |
| 04 |
Số byte |
0x04 (4 byte = 32 bit) |
| 42 A8 |
Giá trị thanh ghi cao |
0x42A8 |
| 00 00 |
Giá trị thanh ghi thấp |
0x0000 |
| 79 32 |
Mã kiểm tra CRC-16 |
0x7932 |
Dữ liệu hợp nhất từ hai thanh ghi là:
16 bit cao = 0x42A8, 16 bit thấp = 0x0000
Ghép lại thành một giá trị 32 bit (mặc định định dạng Big-Endian): 0x42A80000
Biểu diễn nhị phân: 0100 0010 1010 1000 0000 0000 0000 0000
Phân tích theo chuẩn IEEE 754:
• Bit dấu (S) = 0 (số dương)
• Số mũ (E) = 10000101₂ = 133
• Phần trị (M) = 01010000000000000000000₂
Thay vào công thức IEEE 754 để tính giá trị thập phân: 84.0