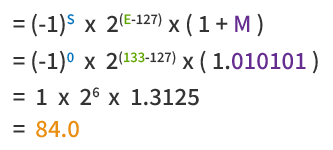1. ¿Qué es un número de punto flotante?
Un número de punto flotante es una forma de representar decimales o números extremadamente grandes usando una cantidad limitada de memoria. Como señala Mitra (2017, párr. 2), "Si bien las operaciones con enteros son más rápidas y están libres de errores de redondeo, los tipos de datos enteros no son adecuados para representar fracciones o valores en un rango extremo."
Ahí es donde entran los números de punto flotante: nos permiten manejar datos numéricos continuos de manera más efectiva. Son especialmente útiles en cálculos científicos, como representar constantes físicas o medir distancias a escala atómica o galáctica. Este tipo de valores son difíciles, si no imposibles, de expresar con enteros. Por eso, prácticamente todos los lenguajes de programación modernos admiten tipos de datos de punto flotante como estándar.
[1]
2. Representación en punto flotante
Los números de punto flotante funcionan de manera similar a la notación científica.
Por ejemplo, el número 12345 en notación científica se escribe como
1.2345 × 10⁴
Aquí, 1.2345 se llama la fracción (o mantisa), y 4 es el exponente.
La notación científica usa base 10 (decimal), mientras que los números de punto flotante usan base 2 (binario).
Tomemos el número 15 como ejemplo:
| Entero (Decimal) |
Notación científica (Decimal) |
Punto flotante (Binario) |
| 15 |
(1.5)10 × 101 |
(1.111)2 × 23 |
Ejemplo: Representar el número 15 como un valor de punto flotante
Paso 1: Convertir 15 a binario
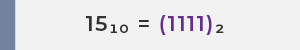
Paso 2: Mover todos los dígitos significativos de la mantisa a la derecha del punto decimal para formar (1.XXXX)₂ × 2ⁿ
Mover el punto decimal tres lugares a la izquierda. Para mantener el mismo valor, elevar la base 2 a la potencia de 3
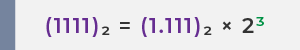
✅ La representación en punto flotante de 15 es :
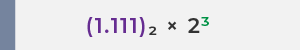
1 ) Formato de punto flotante IEEE 754
Para evitar resultados inconsistentes de números de punto flotante en diferentes plataformas, el IEEE (Instituto de Ingenieros Eléctricos y Electrónicos) introdujo el estándar IEEE 754 en 1985, el cual ha sido ampliamente adoptado desde la década de 1990 para definir cómo se representan y calculan los números de punto flotante (Wikipedia, 2024):
IEEE 754 define:
- Formatos de almacenamiento para números de punto flotante (por ejemplo, Float32 de 32 bits y Float64 de 64 bits).
- Reglas para operaciones de punto flotante (por ejemplo, modos de redondeo, valores especiales como NaN e infinito).
- Casos excepcionales (por ejemplo, desbordamiento, subdesbordamiento y división por cero).
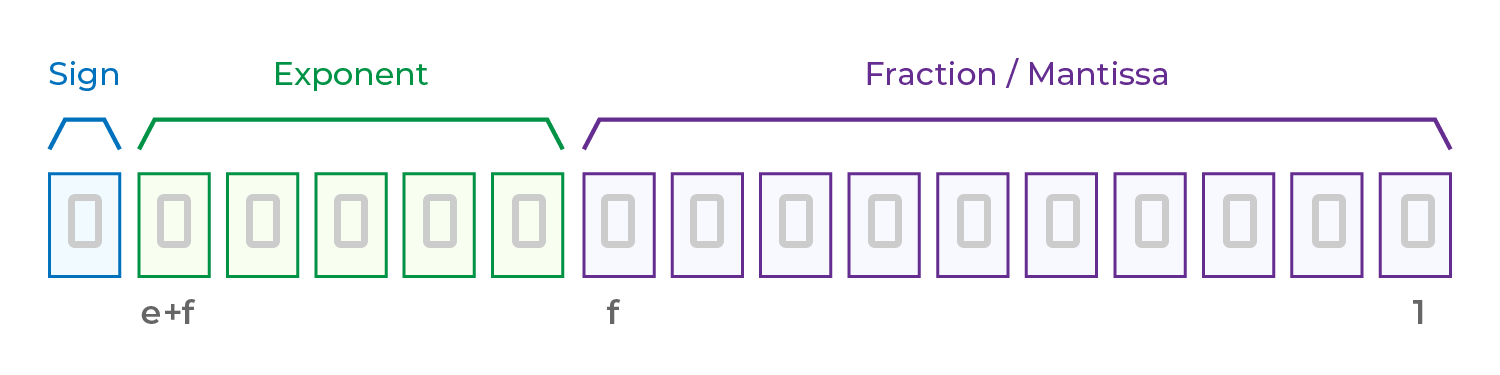
IEEE 754 especifica la estructura de los números de punto flotante como sigue:
Valor = (−1)signo × 2exponente × (1 + fracción)
Bit de signo: 1 bit, determina si el número es positivo o negativo: 0 = positivo / 1 = negativo
Sesgo del exponente: Se utiliza para controlar el rango del valor (como potencias de 2), calculado como el exponente menos el sesgo.
Fracción (Mantisa): Representa "1 + parte fraccionaria" y almacena los dígitos significativos (similar a "1.XX" en notación científica).
2 ) Precisión en punto flotante: Float32 y Float64
La representación en punto flotante del número
15 es
(1.111)₂ × 2³, lo cual se escribe como
(−1)⁰ × 2³ × (1.111)₂
Esto sigue el formato normalizado de IEEE 754. Cuando las computadoras almacenan números de punto flotante, los codifican según el estándar IEEE 754 utilizando ya sea precisión simple (Float32) o precisión doble (Float64).
Precisión simple
Al almacenar un número de punto flotante, el 1 principal es implícito, por lo que solo se guarda la parte fraccionaria en lugar de toda la mantisa.
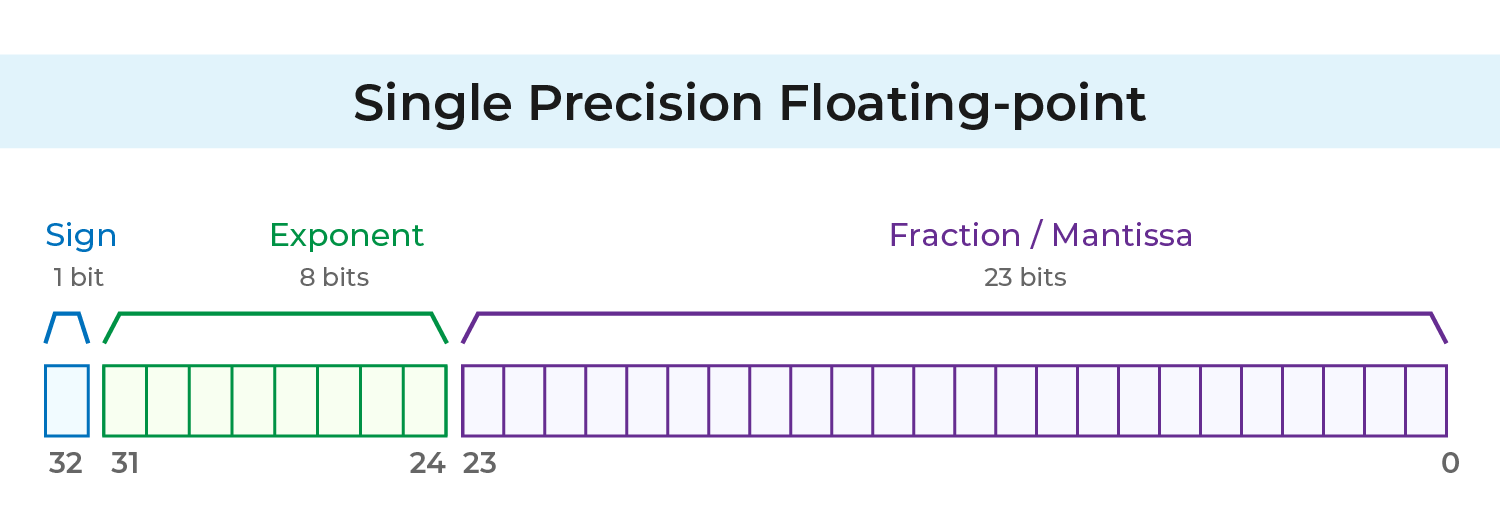
IEEE 754 en precisión simple utiliza 32 bits en total:
1 bit: Bit de signo
8 bits: Exponente (m)
23 bits: Fracción (f)
En precisión simple, el exponente se sesga con 127 para evitar almacenar un signo negativo. La computadora almacena
m + 127 en lugar de
m. Por lo tanto, el valor máximo del exponente es 127 y el mínimo es −126.
(Grainger College of Engineering, 2019)
* Para ejemplos de cálculo, consulte la siguiente sección.
Precisión doble
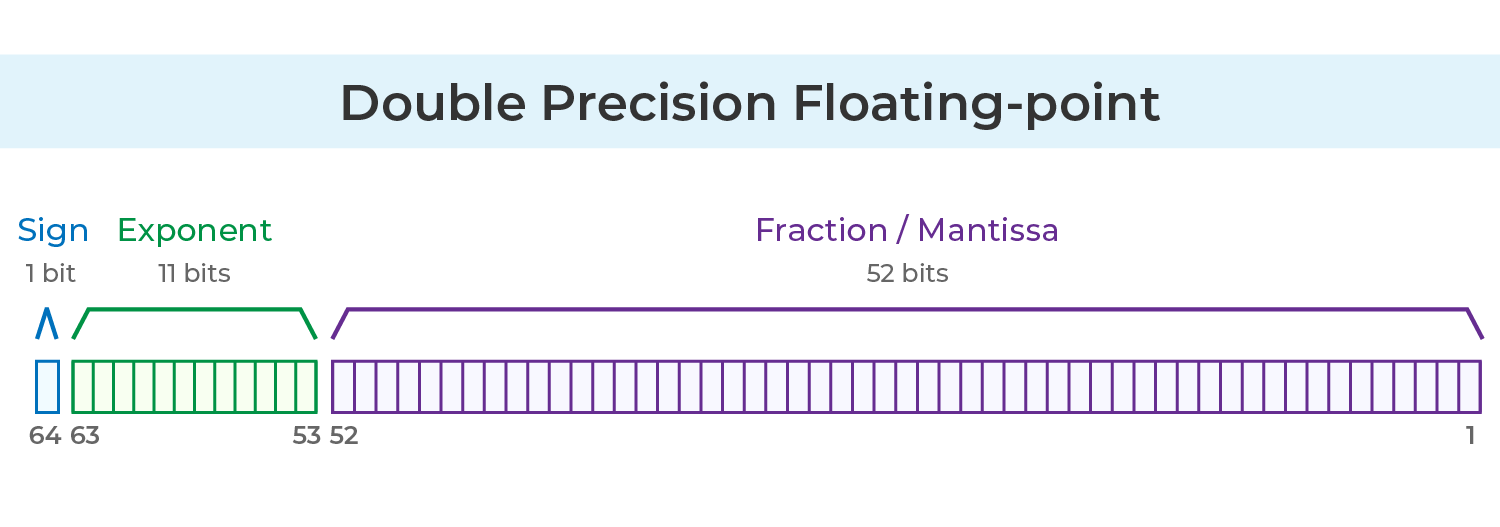
IEEE 754 en precisión doble utiliza 64 bits en total:
1 bit: Bit de signo
11 bits: Exponente (m)
52 bits: Parte fraccionaria (f)
En precisión doble, el exponente se sesga con 1023 para evitar almacenar un signo negativo. La computadora almacena m + 1023 en lugar de m. Por lo tanto, el valor máximo del exponente es 1023 y el mínimo es −1022.
(Grainger College of Engineering, 2019)
Comparación de características: Float32 vs Float64
| Característica |
Float32 (Precisión simple) |
Float64 (Precisión doble) |
| Longitud de bits |
32 bits |
64 bits |
| Longitud de la fracción |
23 bits (aprox. 7–8 cifras decimales |
52 bits (aprox. 15–16 cifras decimales |
| Longitud del exponente |
8 bits (sesgo: 127) |
11 bits (sesgo: 1023) |
| Rango de valores |
Aprox. 10⁻³⁸ ~ 10³⁸ |
Aprox. 10⁻³⁰⁸ ~ 10³⁰⁸ |
| Uso de memoria |
4 bytes (32-bit) |
8 bytes (64-bit) |
| Rendimiento |
Más rápido (ideal para gráficos, entrenamiento de IA) |
Más lento pero más preciso (mejor para cálculos científicos) |
| Aplicaciones comunes |
• Desarrollo de videojuegos, procesamiento gráfico (cómputo en GPU)
• Aprendizaje automático (por ejemplo, precisión mixta en TensorFlow)
• Conjuntos de datos grandes con baja necesidad de precisión |
• Cómputo científico y simulaciones (por ejemplo, predicción meteorológica, modelado físico)
• Cálculos financieros (para evitar errores de redondeo)
• Cálculos numéricos de alta precisión (por ejemplo, aplicaciones de ingeniería)
|
3. 32-bit Floating-Point Calculation Example
| Formato de precisión simple (Float32, 32 bits) |
| Componente |
Longitud en bits |
Descripción |
Bit de signo (S)
|
1 bit |
0 (positive) |
| Exponente (E) |
8 bits |
3 + 127 = 130 = 10000010₂ |
| Fracción (M) |
23 bits |
11100000000000000000000 (se omite el 1 inicial, solo se almacena 111) |
| Almacenamiento |
32 bits |
0 10000010 11100000000000000000000 |
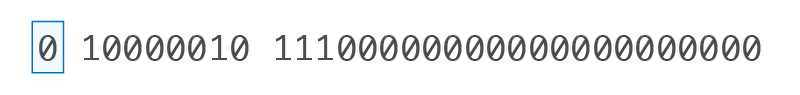• Bit de signo (S): 0
(−1)⁰ = 1 (indica un número positivo)
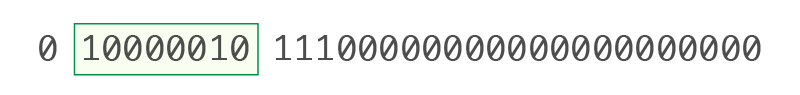• Exponente (E) (Bits 2–9): 10000010
Convertir a decimal: 10000010₂ = 130₁₀
*IEEE 754 utiliza un sesgo de 127
130 - 127 = 3
Por lo tanto, el exponente = 3, lo que significa 2³
(*IEEE 754 utiliza un sesgo para representar exponentes. Para precisión simple (32 bits), el campo de exponente usa 8 bits. Según la definición IEEE 754, el sesgo se calcula como: Sesgo = 2⁸⁻¹ − 1 = 127)
• Fracción (M): 11100000000000000000000
Según IEEE 754, la fracción usa la forma normalizada “1 + valor fraccionario”, por lo que el valor real es: 1.11100000000000000000000₂
convertir a decimal:
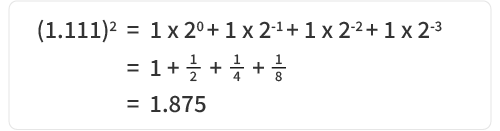
El formato de punto flotante IEEE 754 se define como:
Valor = (−1)signo × 2exponente × (1 + fracción)
= (−1)0 × 23 × (1 + 0.875)
= 15
4. Acceso y conversión de números de punto flotante en Modbus
En la comunicación Modbus, los datos se almacenan en registros, y cada registro tiene una longitud de 16 bits. Sin embargo, para representar un número de punto flotante de precisión simple se requieren 32 bits. Para manejar esto dentro de la arquitectura Modbus, los datos que superan los 16 bits deben abarcar varias direcciones de registro consecutivas. Por lo tanto, un valor de punto flotante de 32 bits necesita ocupar dos registros adyacentes.
El protocolo Modbus especifica el uso del formato Big-Endian para la transmisión de valores multibyte. En el orden Big-Endian, el byte más significativo se transmite primero. Por ejemplo, el valor hexadecimal de 16 bits 0x1234 se transmite en el bus como 0x12 seguido de 0x34. (Modbus Organization, 2006)
[4]
1 ) Cómo almacena Modbus un número de punto flotante de 32 bits
¿Cómo se almacena el número de punto flotante 84.0 en Modbus?
• Convertir al formato de punto flotante de precisión simple IEEE 754:
La representación binaria de precisión simple (32 bits) IEEE 754 de 85.625 es:
01000010101010000000000000000000₂
• Convertir a hexadecimal: 0x42A80000
• Almacenamiento en Modbus (formato Big-Endian):
Dado que cada registro Modbus es de 16 bits, un número flotante de 32 bits se divide en dos registros:
Registro alto (primeros 16 bits): 0x42A8
Registro bajo (últimos 16 bits): 0x0000
2 ) Cómo decodificar valores Modbus a números de punto flotante
Ejemplo:
Dirección del dispositivo (ID del esclavo): 0x01
Código de función: 0x03 (Leer registros de retención)
Dirección de registro de inicio: 0x1000
Número de registros a leer: 0x0002 (ya que un flotante de 32 bits ocupa dos registros de 16 bits)
➤ Solicitud de transmisión Modbus (TX - El maestro envía datos):
01 03 10 00 00 02 C5 CD
| Byte |
Descripción |
Valor |
| 01 |
Dirección del dispositivo (ID del esclavo) |
0x01 |
| 03 |
Código de función (Leer registros de retención) |
0x03 |
| 10 00 |
Dirección de inicio (0x1000) |
0x1000 |
| 00 02 |
Cantidad de registros (Leer 2) |
0x0002 |
| C5 CD |
Suma de verificación CRC-16 |
0xC5CD |
➤ Respuesta del dispositivo Modbus (RX - El esclavo responde):
01 03 04 42 A8 00 00 79 32
| Byte |
Descripción |
Valor |
| 01 |
Dirección del dispositivo (ID del esclavo) |
0x01 |
| 03 |
Código de función (Leer registros de retención) |
0x03 |
| 04 |
Cantidad de bytes |
0x04 (4 bytes = 32 bits) |
| 42 A8 |
Valor del registro alto |
0x42A8 |
| 00 00 |
Valor del registro bajo |
0x0000 |
| 79 32 |
Suma de verificación CRC-16 |
0x7932 |
Como se muestra, los datos de los registros combinados son:
Registro alto de 16 bits = 0x42A8, Registro bajo de 16 bits = 0x0000
Combinado en un valor de 32 bits (formato Big-Endian por defecto): 0x42A80000
Representación binaria: 0100 0010 1010 1000 0000 0000 0000 0000
Descomposición IEEE 754:
• Bit de signo (S) = 0 (positivo)
• Exponente (E) = 10000101₂ = 133
• Fracción (M) = 01010000000000000000000₂
Sustituyendo en la fórmula IEEE 754, obtenemos el valor decimal:
84.0
